Peano’s Arithmetic
As a reminder, here are Peano’s axioms, which concern the successor function ![]() , which intuitively “adds
, which intuitively “adds ![]() ” to each natural integer.
” to each natural integer.
These axioms allow us to reconstruct the whole arithmetic structure of the set ![]() of natural integers, and from naive set theory, all natural mathematical objects and structures.
of natural integers, and from naive set theory, all natural mathematical objects and structures.
Axiom 1
![]() is not the successor of any natural number. In other words, there is no natural number
is not the successor of any natural number. In other words, there is no natural number ![]() such that
such that ![]() .
.
This axiom says in particular that the function ![]() is not surjective, since the number
is not surjective, since the number ![]() has no antecedent by
has no antecedent by ![]() .
.
Axiom 2
If two natural numbers have the same successor, then they are equal. In other words, for all natural numbers ![]() , if
, if ![]() then
then ![]() .
.
We can reformulate this axiom by saying that the successor application is injective. It thus defines a bijection from ![]() onto
onto ![]() . We recognise here the characterisation of an infinite set.
. We recognise here the characterisation of an infinite set.
Proposition 1
The set ![]() of natural numbers is infinite.
of natural numbers is infinite.
Axiom 3 [Principle of induction (or recursion)]
If ![]() is a subset of
is a subset of ![]() such that:
such that:
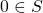
- for all
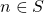 ,
, 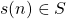 (“induction step”),
(“induction step”),
then we have ![]() .
.
This principle expresses intuitively that the set ![]() is entirely \og browsed” if we enumerate it starting from
is entirely \og browsed” if we enumerate it starting from ![]() and add each successive natural number, indefinitely.
and add each successive natural number, indefinitely.
We can deduce the determination of the image of ![]() :
:
Proposition 2
If we admit the induction principle, then the image of ![]() is
is ![]() , the set of non-zero natural numbers.
, the set of non-zero natural numbers.
Demonstration
Let ![]() be the set
be the set ![]() . If we show that
. If we show that ![]() , then any non-zero natural number is in the image of
, then any non-zero natural number is in the image of ![]() , so
, so ![]() . By definition, we have
. By definition, we have ![]() , and suppose that
, and suppose that ![]() is a natural number, and that
is a natural number, and that ![]() . By definition, the natural integer
. By definition, the natural integer ![]() is in
is in ![]() ! By the induction principle, the set
! By the induction principle, the set ![]() is the whole set
is the whole set ![]() , and the proposition is proved.
, and the proposition is proved. ![]()