M A T H E S I S
A Conceptual Approach to Mathematical Science
The axiomatic construction of natural arithmetic
Natural arithmetic is the science of natural numbers: it is based on addition, multiplication, natural order and divisibility. Now, all these operations and relations are defined on the basis of the single successor function, whose properties are brought together in...
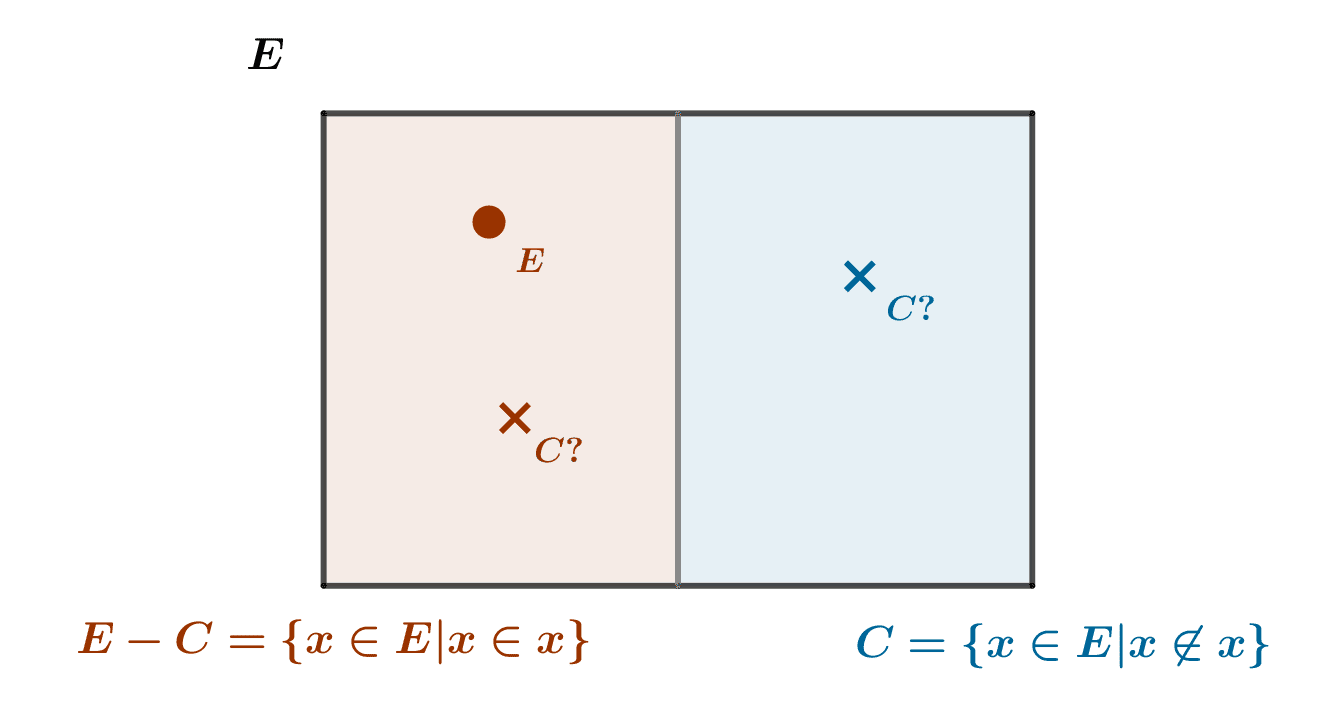
Russell’s paradox and the emergence of class theory
Russell's paradox or antinomy is a very simple paradox in naive set theory, which arises when one tries to define a "set of all sets". Its resolution relies on the introduction of the notion of class and the distinction of sets among classes. Thanks to class theory,...
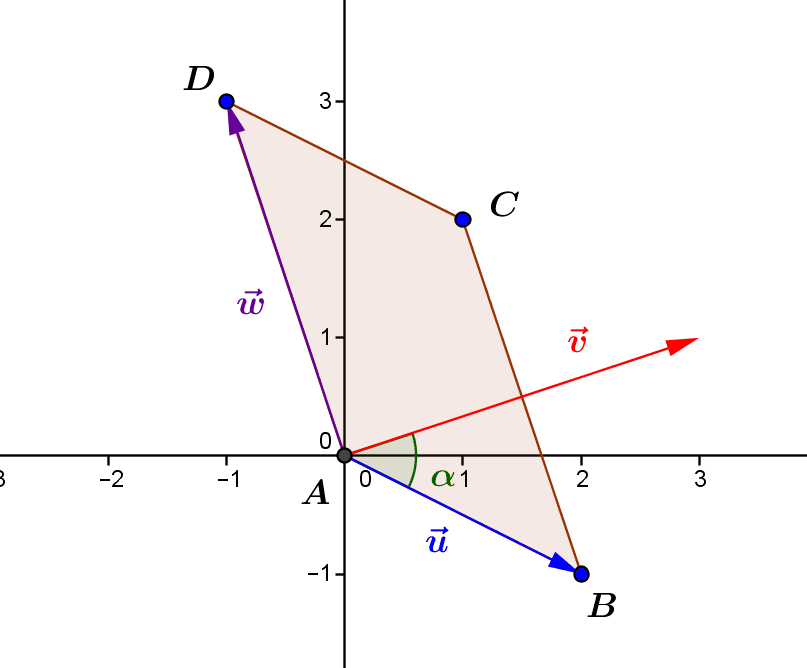
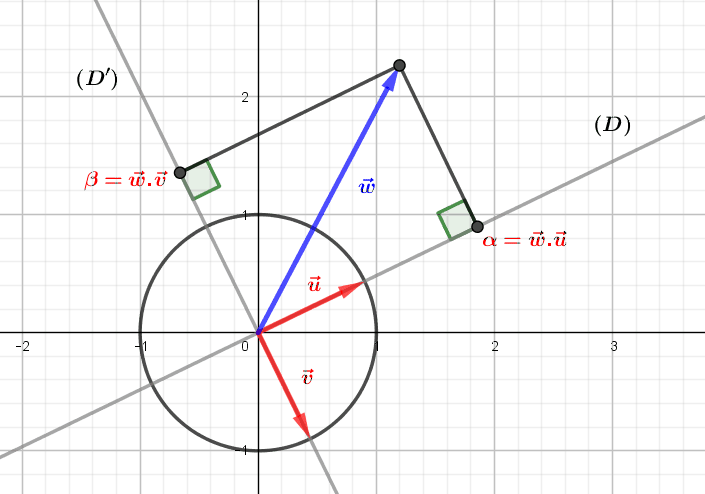
The natural scalar (or dot) product: a numerical combination of vectors
The scalar or dot product of two vectors in real space is a real number that takes into account the direction, sense and magnitude of both vectors. 1.The natural scalar product in the Euclidean plane 1.1.From the distance between two points to the scalar product In...
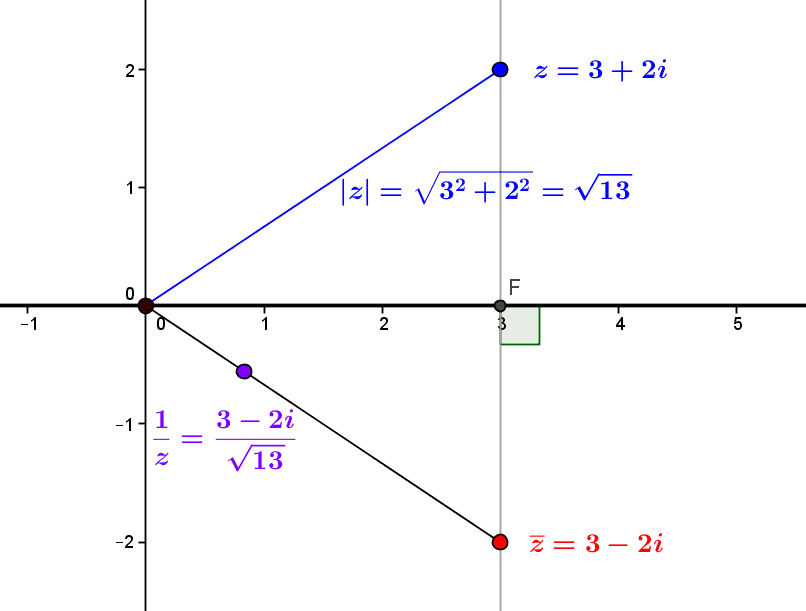
Gaussian integers: an imaginary arithmetic
Gaussian integers are complex numbers with integer coordinates. Thanks to their norm, a kind of integer measure of their size, we can describe some of their arithmetic properties. In particular, we can determine which are the usual prime numbers that "remain" prime as...
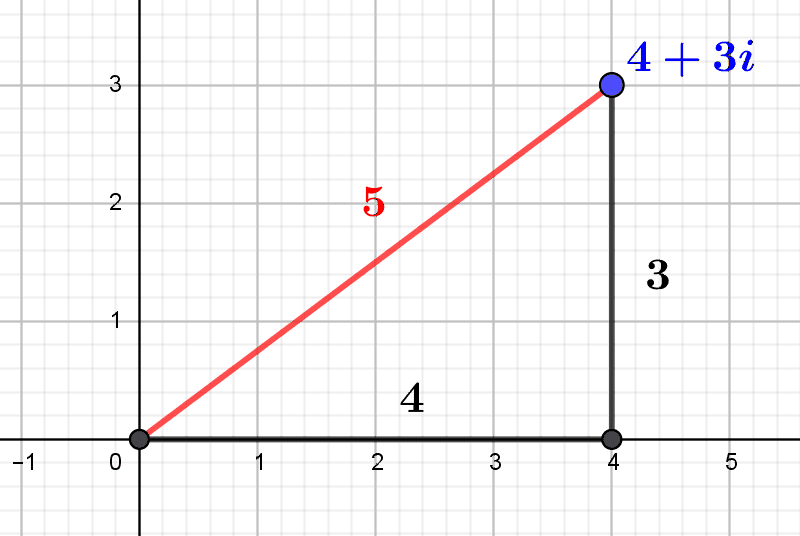
What is a complex number? A simple geometric approach
There are various ways of defining complex numbers. The most direct way is to look at them as points or vectors of the Euclidean plane. Addition and multiplication are then defined using the coordinates. 1. The set \(\mathbb C\) of complex numbers 1.1. A complex...
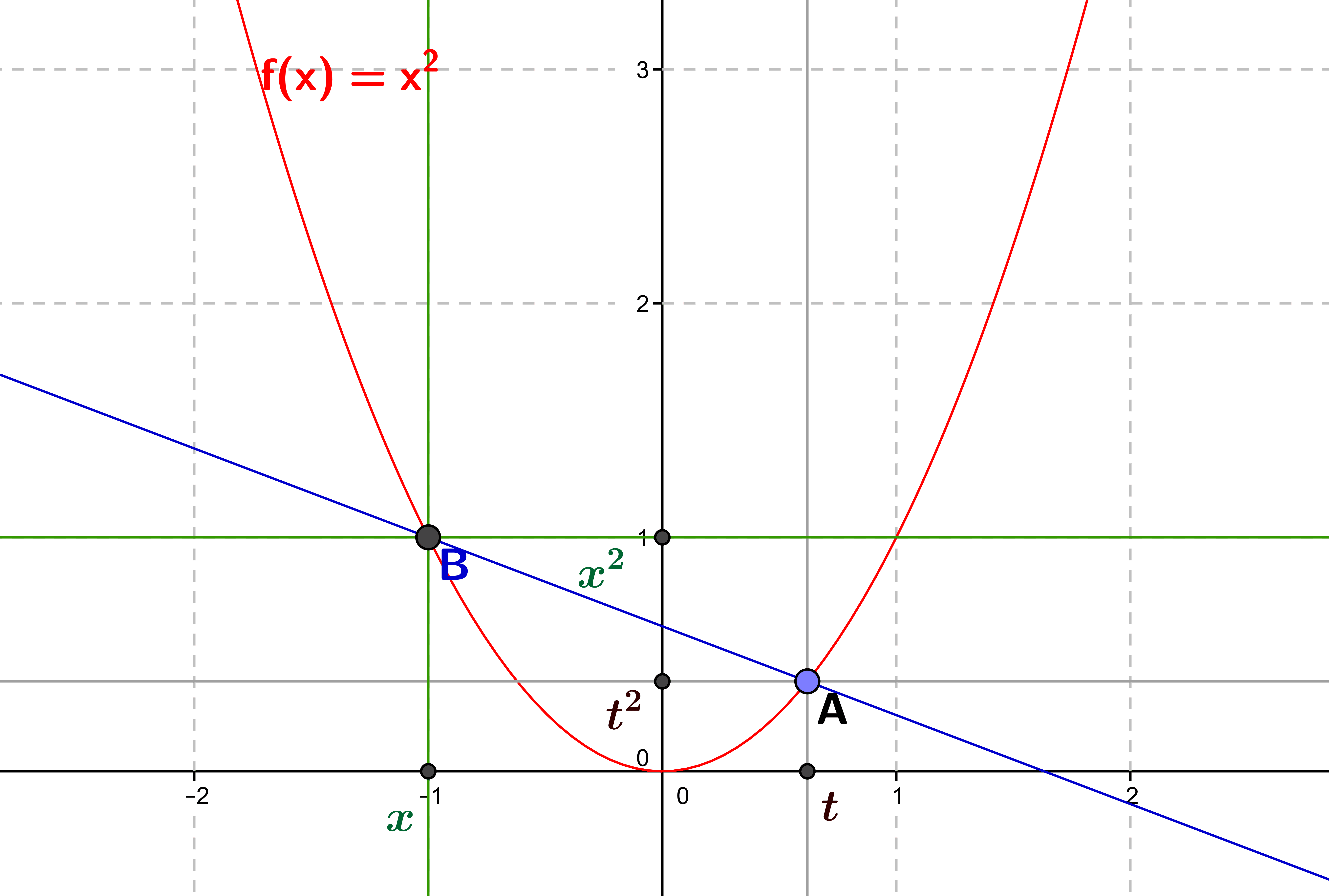
The derivative of a function: definition and geometric interpretation
The derivative of a function is its instantaneous variation, i.e. the slope of the tangent to the graphical representation of the function at that point. 1. General idea: an instantaneous variation We place ourselves here in the framework of functions of a real...
Linear transformations of the plane: determinant, bases and inversion
The linear transformations of the Euclidean plane are the invertible linear applications, i.e. of non-zero determinant. They allow us to move from one basis of the plane to another, and the orthogonal transformations, i.e. the vectorial isometries, exchange the...
The bases of the Euclidean plane: vectors and coordinates
The representation of the Euclidean plane as the Cartesian product \(\mathbb R^2\) allows us to decompose any vector of the plane into two coordinates, its abscissa and its ordinate. This decomposition is linked to a particular and natural "representation system",...
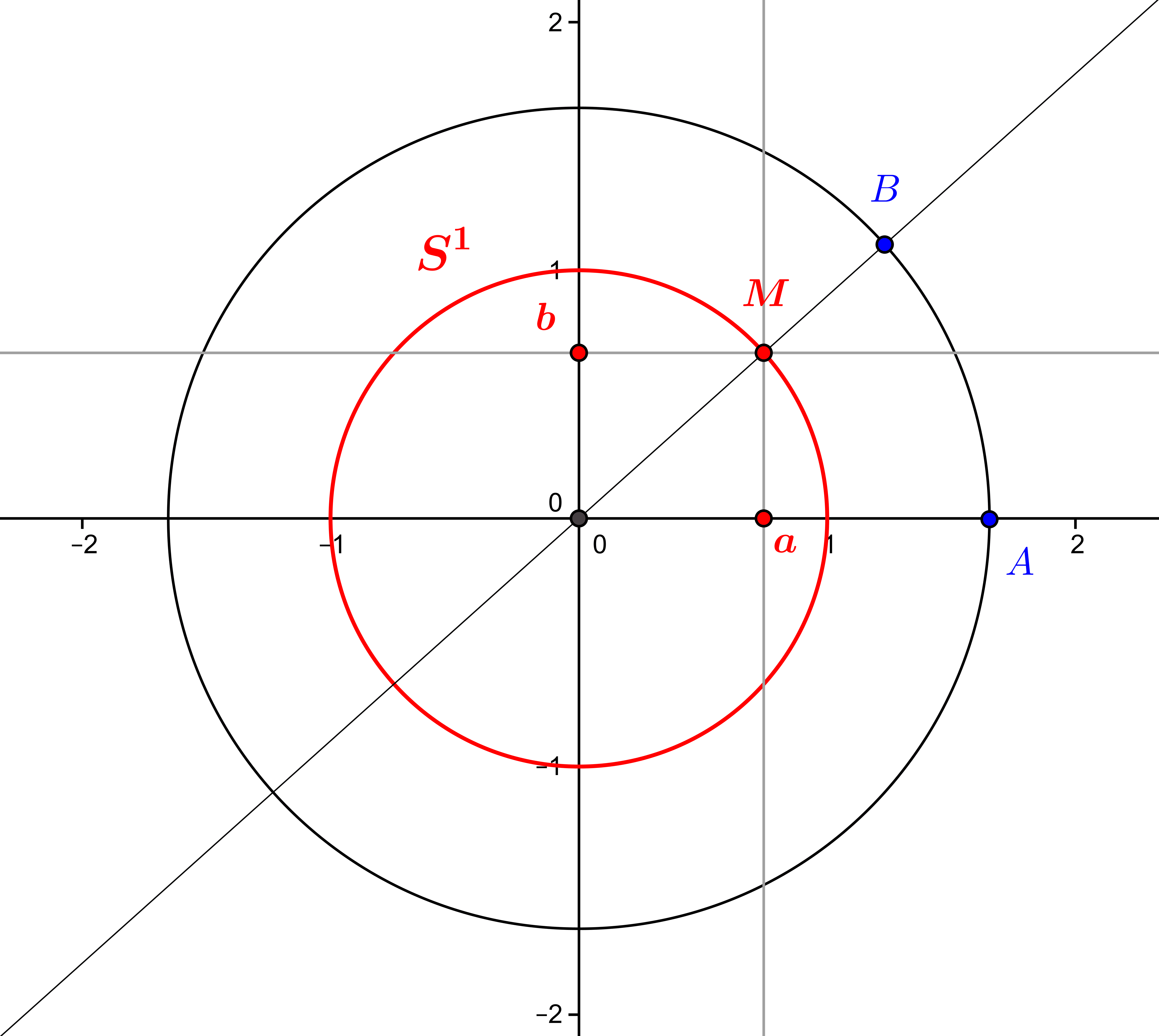
Vector rotations of the plane: the analytical approach
The vector rotations of the plane (i.e. centred in the origin), are derived analytically (by coordinates) as linear applications of determinant \(1\), which makes it possible to characterise them integrally and to identify them with the points of the trigonometric...
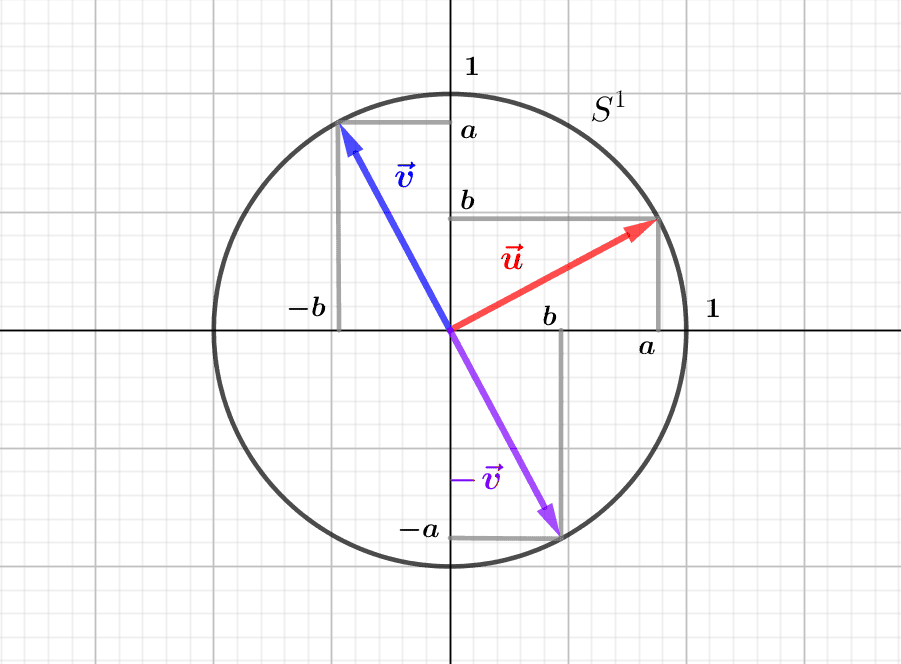
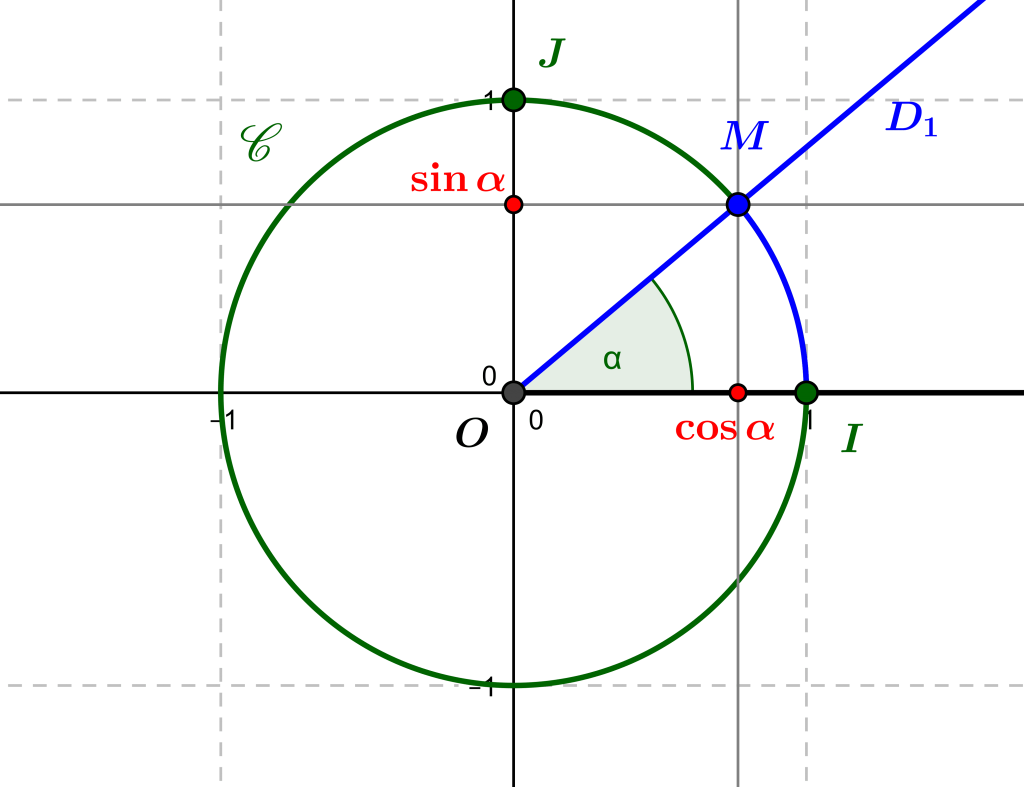
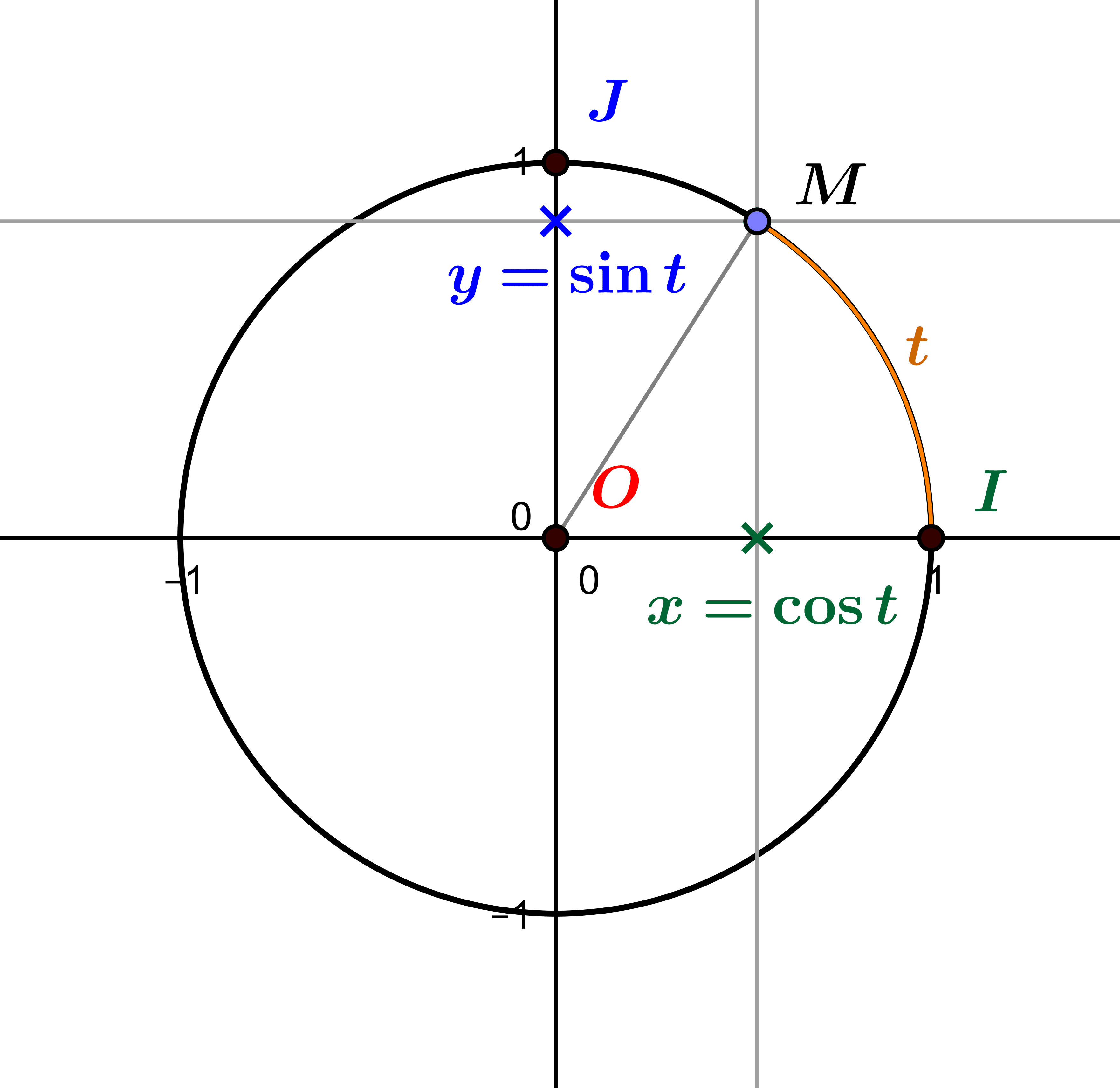
The Trigonometric Circle: where Pythagoras meets Thales
The trigonometric circle allows us to define the cosine, sine and tangent of an oriented angle, and to give an interpretation through Thales' and Pythagoras' theorems. Introduction: trigonometry and functions Trigonometry is the study of the relationships between...
Drawing a circle on the plane: equation and parameters
The definition of a circle is simple: it is a set of points located at the same distance from a given point. This distance is called the radius and this point is called the centre of the circle. The circle with centre \((-1,-3/2)\) and radius \(\sqrt 6\) 1. Circles as...
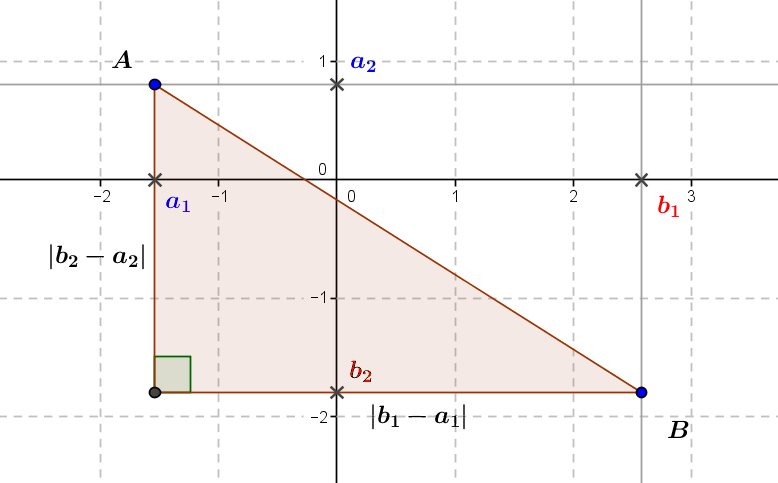
The Euclidean Plane: Ancient Geometry and Modern Approach
From Descartes' analytic approach, which consists in introducing coordinates to represent the points of the plane, and from Cauchy's construction of the real numbers, we can give a modern representation of the euclidean plane from which we recover Euclid's geometric...
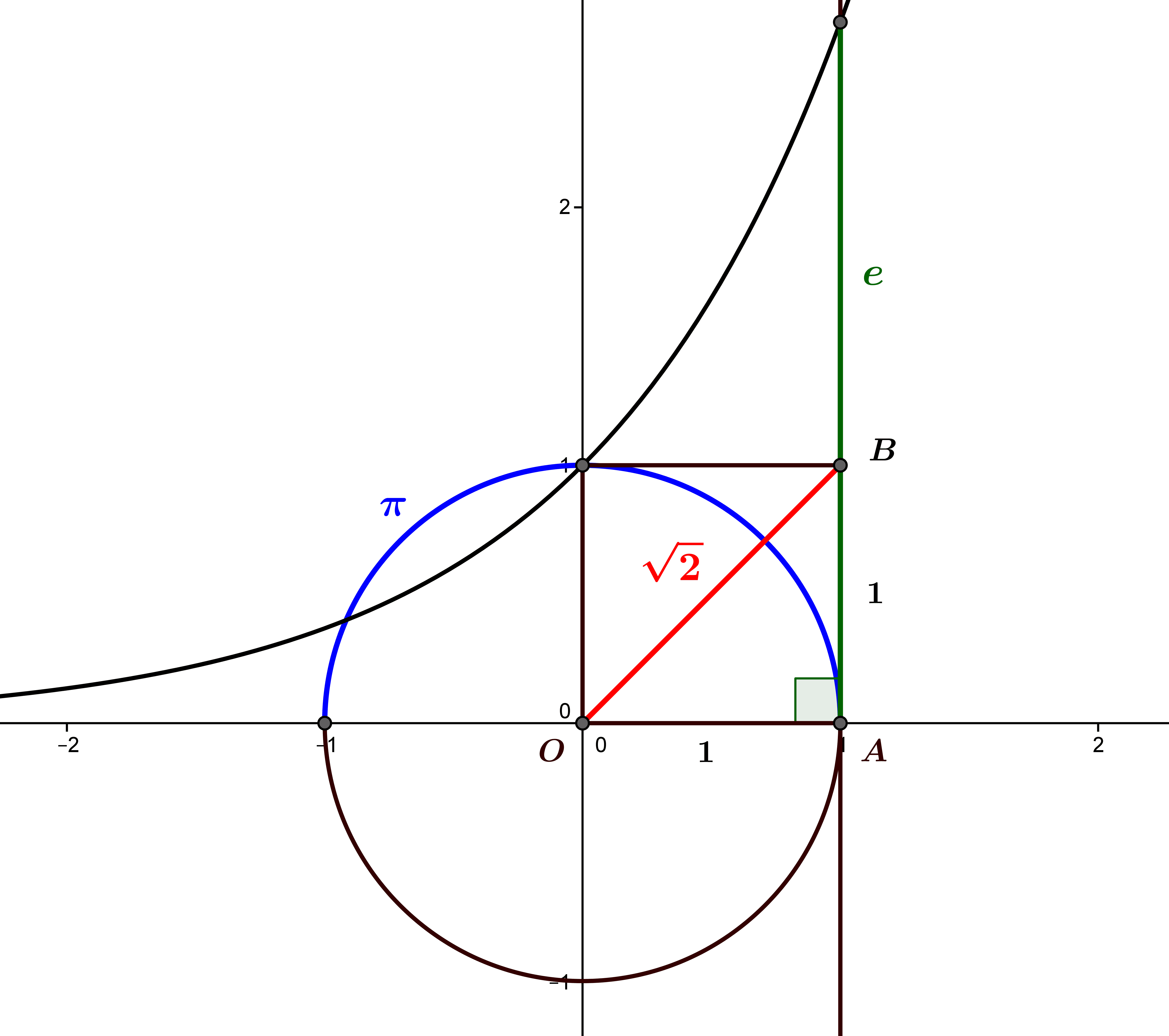
What is a real number ? Cauchy’s fantastic construction
The real numbers are all the "quantities" that we can order, and we can "construct" them in various ways thanks to set theory. "Numbers govern the world." Pythagoras The real numbers idealise all the "points" of the geometrical line, or from the arithmetic point of...
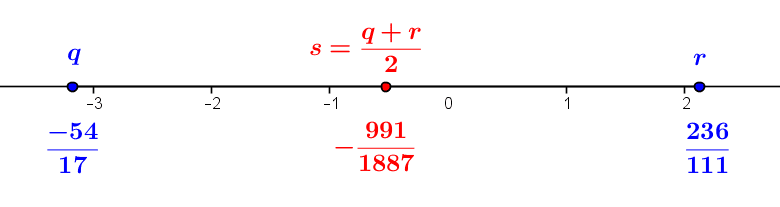
What is a rational number? Quotients of numbers and sets
1.The intuition of rational numbers Rational numbers, i.e. "fractional" numbers, such as \(-\frac 1 2, \frac{27}{4}, \frac{312}{-6783},\ldots\), form an intuitive set which we note \(\mathbb Q\). It is an extension of the set \(\mathbb Z\) of integers (see What is an...
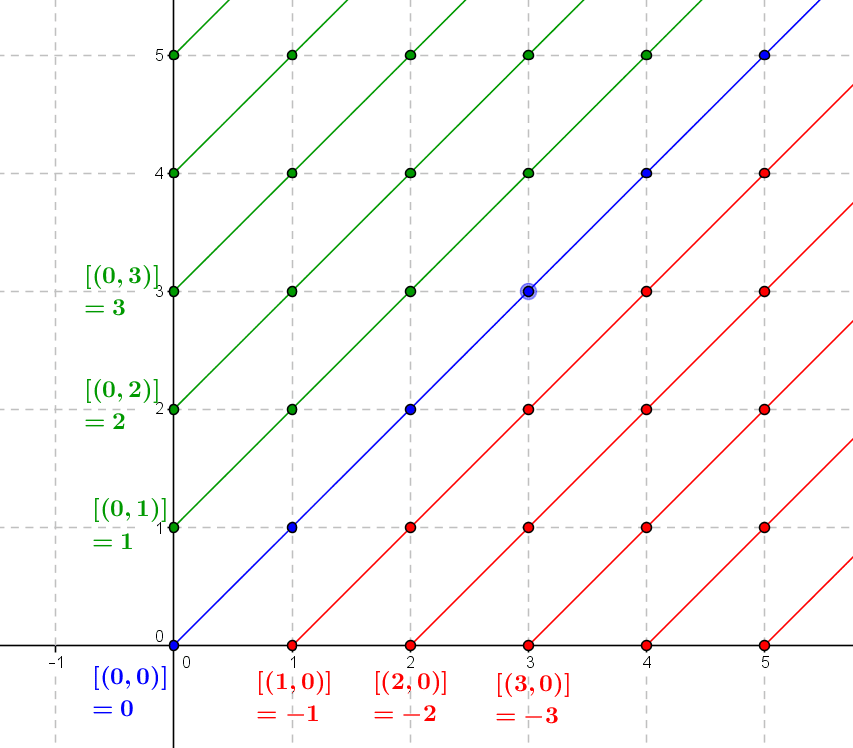
What is an integer ? A crafty representation
Integers are an extension of the natural numbers where the existence of subtraction provides a more appropriate framework for certain questions of arithmetic. They can be described axiomatically, but can also be constructed from the set of natural numbers and some...
What is a natural number? Defining or axiomatising
Mathematical science does not seek to define the notion of a natural number, but to understand the set of natural numbers. "Natural numbers have been made by God, everything else is the work of men". Leopold Kronecker 1.We don't define the natural numbers, but we can...
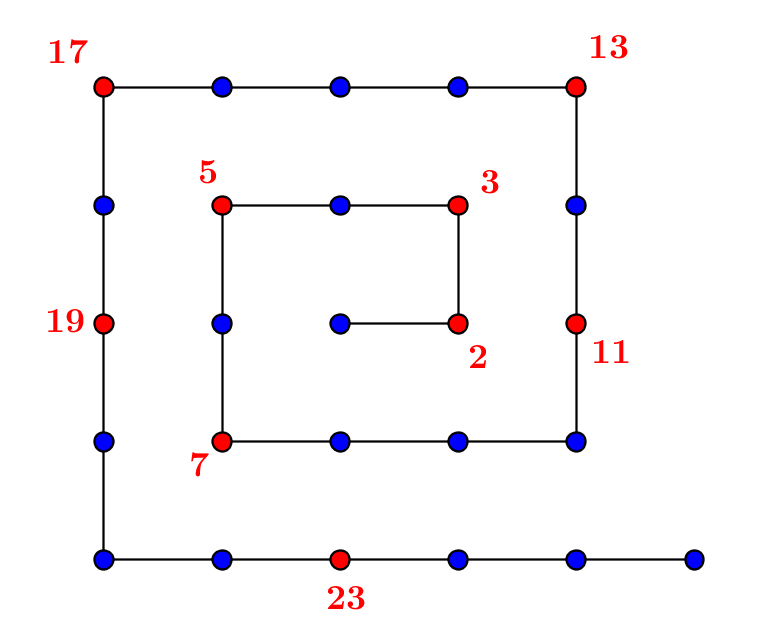
An infinity of prime numbers : Euclid’s theorem
The prime natural numbers are those which have no divisors other than 1 and themselves. They exist in infinite number by Euclid's theorem, which is not difficult to prove. 1.Prime numbers 1.1.Divisors and primes A prime number is a non-zero natural number (see What is...
Finiteness and Mathematical Infinity : Comparing and Enumerating
A finite set is a set that can be counted using the natural numbers \(1,\ldots,n\) for a certain natural number \(n\). But what is counting ? And then, what is an infinite set? 1.Comparing sets : the notion of bijection The notions of finite set and infinite set, and...
What is a set? Founding mathematics in intuition
Naive set theory or "potato science" is the natural (and understandable!) foundation of mathematical science. "I know what time is. If you ask me, I don't know anymore." Augustine. This insightful quote from Augustine emphasises that there are concepts that we...