
by M4t_6_onL | Jul 10, 2023 | Logic, Number theory, Set theory
Natural arithmetic is the science of natural numbers: it is based on addition, multiplication, natural order and divisibility. Now, all these operations and relations are defined on the basis of the single successor function, whose properties are brought together in...
by M4t_6_onL | May 8, 2023 | Set theory
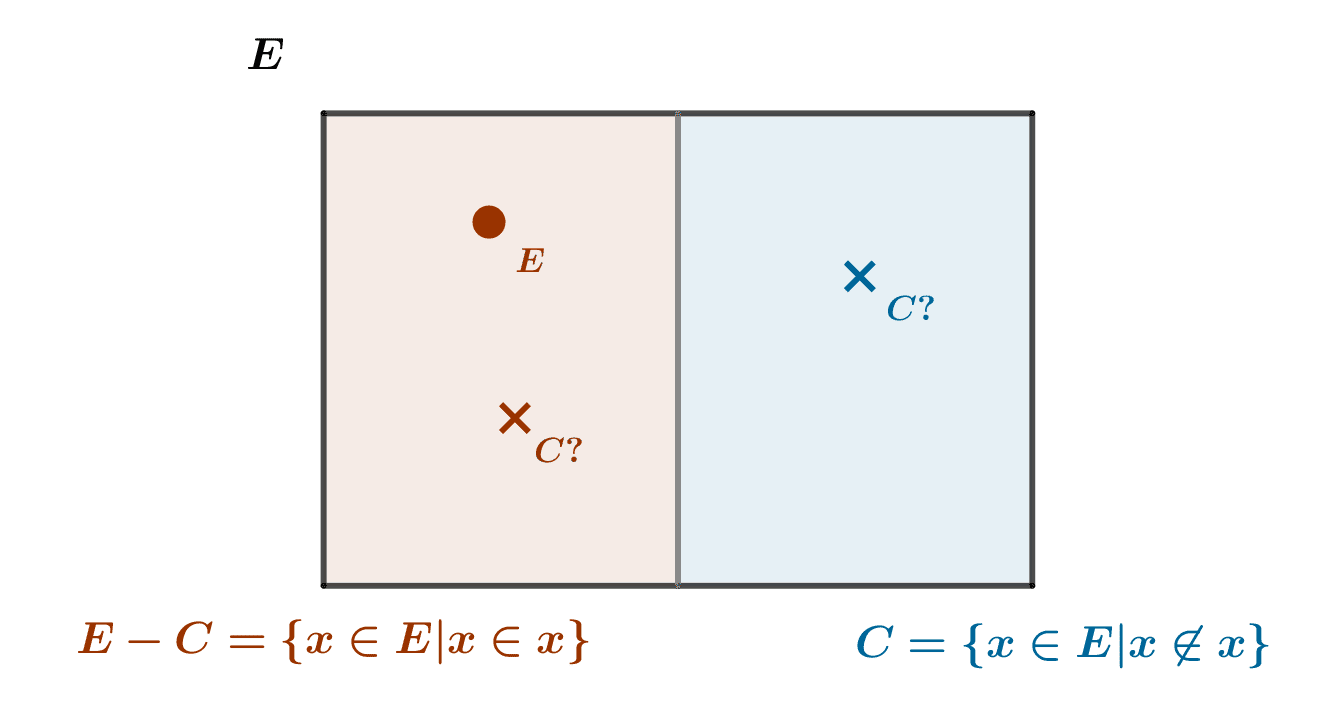
Russell’s paradox or antinomy is a very simple paradox in naive set theory, which arises when one tries to define a “set of all sets”. Its resolution relies on the introduction of the notion of class and the distinction of sets among classes. Thanks...
by M4t_6_onL | Aug 15, 2021 | Number theory, Set theory
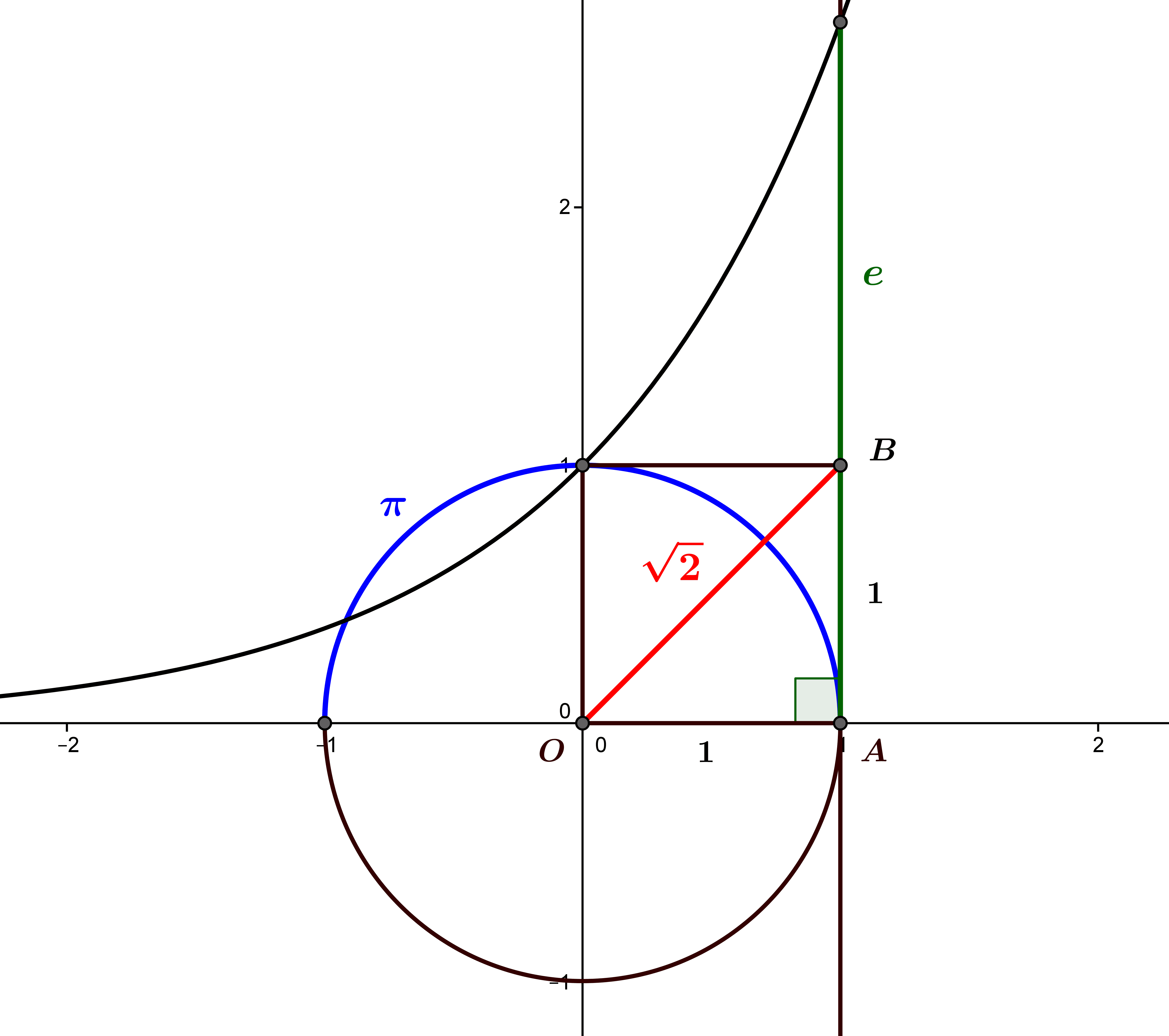
The real numbers are all the “quantities” that we can order, and we can “construct” them in various ways thanks to set theory. “Numbers govern the world.” Pythagoras The real numbers idealise all the “points” of the...
by M4t_6_onL | Aug 6, 2021 | Number theory, Set theory
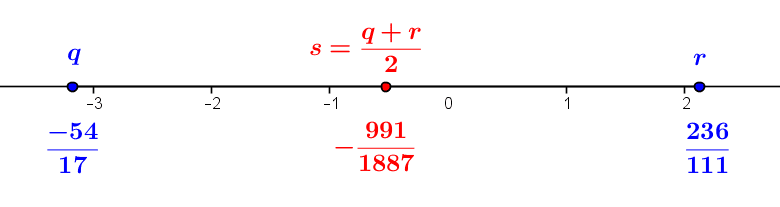
1.The intuition of rational numbers Rational numbers, i.e. “fractional” numbers, such as \(-\frac 1 2, \frac{27}{4}, \frac{312}{-6783},\ldots\), form an intuitive set which we note \(\mathbb Q\). It is an extension of the set \(\mathbb Z\) of integers (see...
by M4t_6_onL | Jul 30, 2021 | Number theory, Set theory
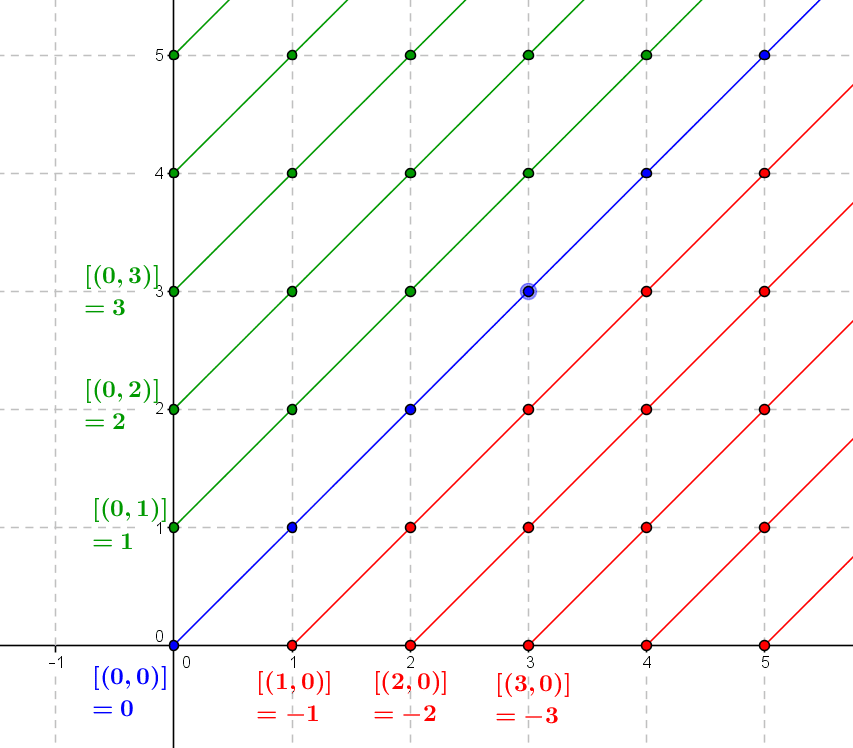
Integers are an extension of the natural numbers where the existence of subtraction provides a more appropriate framework for certain questions of arithmetic. They can be described axiomatically, but can also be constructed from the set of natural numbers and some...
by M4t_6_onL | Jul 30, 2021 | Number theory, Set theory
Mathematical science does not seek to define the notion of a natural number, but to understand the set of natural numbers. “Natural numbers have been made by God, everything else is the work of men”. Leopold Kronecker 1.We don’t define the natural...






