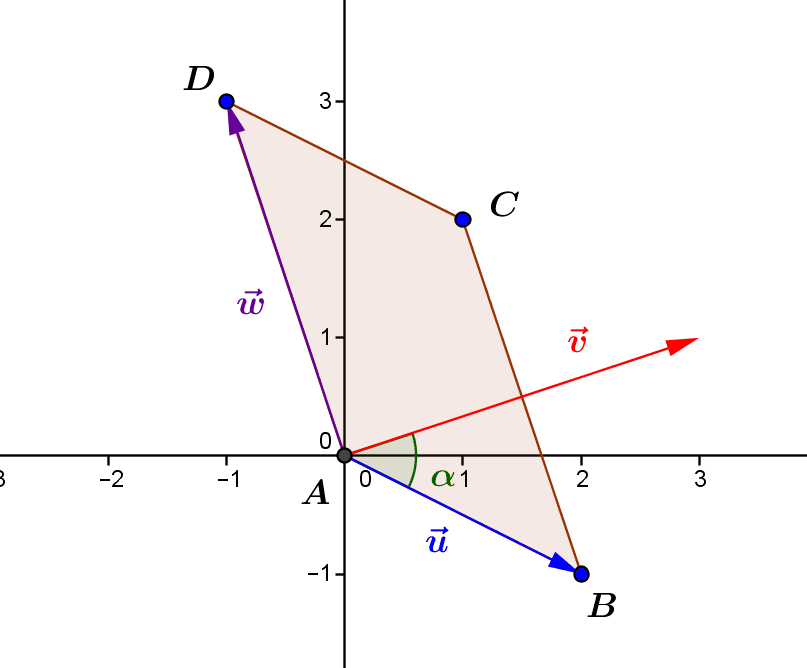
by M4t_6_onL | Dec 8, 2022 | Algebra, Geometry
The scalar or dot product of two vectors in real space is a real number that takes into account the direction, sense and magnitude of both vectors. 1.The natural scalar product in the Euclidean plane 1.1.From the distance between two points to the scalar product In...
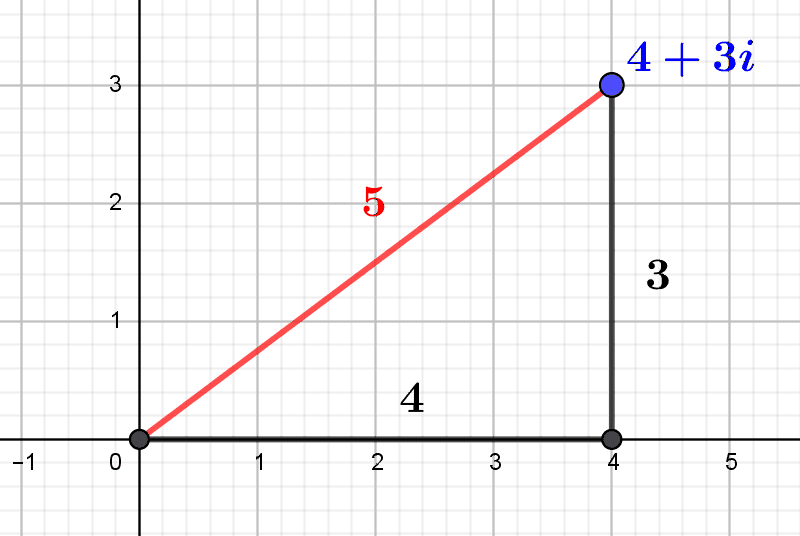
by M4t_6_onL | Oct 24, 2022 | Algebra, Number theory
Gaussian integers are complex numbers with integer coordinates. Thanks to their norm, a kind of integer measure of their size, we can describe some of their arithmetic properties. In particular, we can determine which are the usual prime numbers that...
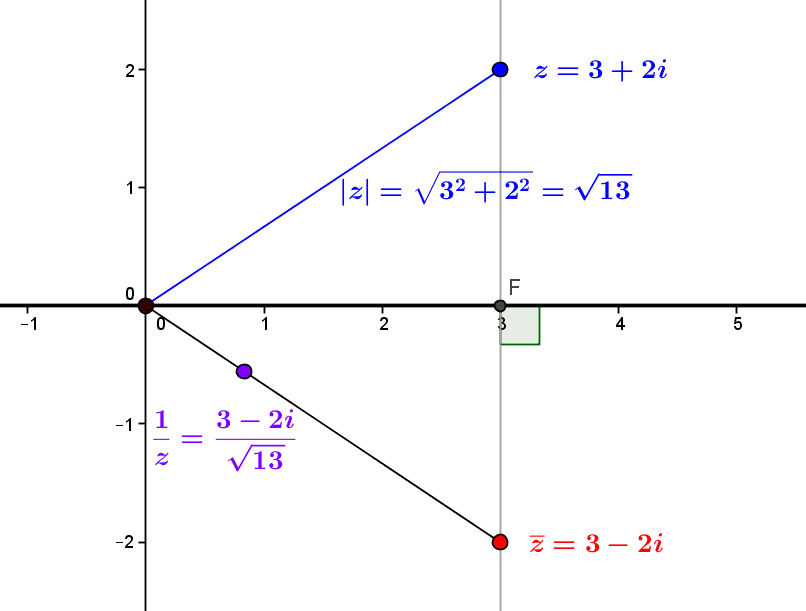
by M4t_6_onL | Aug 1, 2022 | Algebra, Number theory
There are various ways of defining complex numbers. The most direct way is to look at them as points or vectors of the Euclidean plane. Addition and multiplication are then defined using the coordinates. 1. The set \(\mathbb C\) of complex numbers 1.1. A complex...
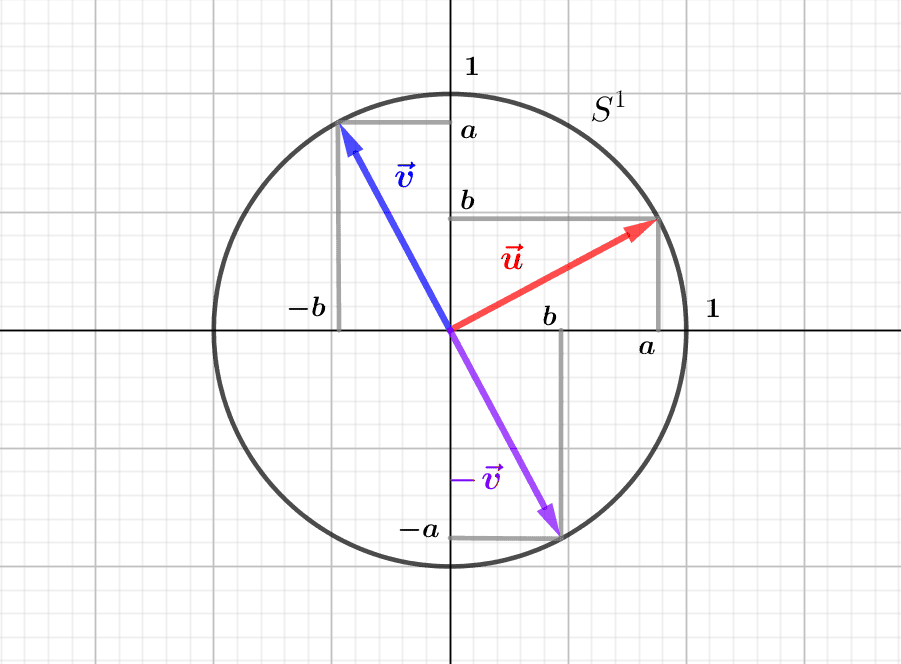
by M4t_6_onL | Apr 28, 2022 | Algebra, Geometry
The linear transformations of the Euclidean plane are the invertible linear applications, i.e. of non-zero determinant. They allow us to move from one basis of the plane to another, and the orthogonal transformations, i.e. the vectorial isometries, exchange the...
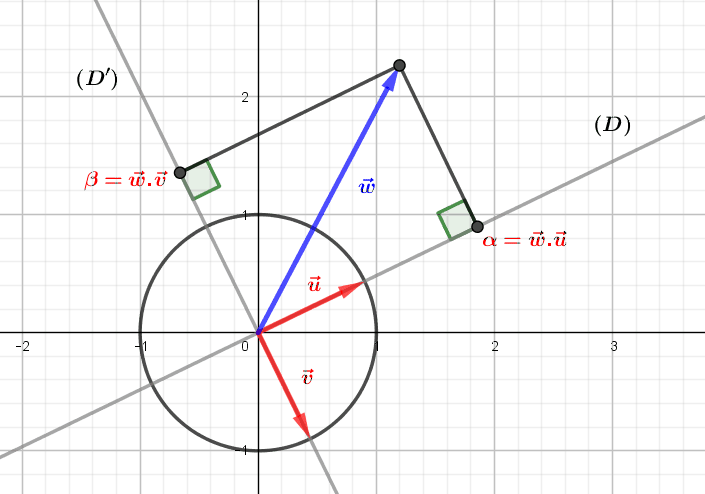
by M4t_6_onL | Apr 23, 2022 | Algebra, Geometry
The representation of the Euclidean plane as the Cartesian product \(\mathbb R^2\) allows us to decompose any vector of the plane into two coordinates, its abscissa and its ordinate. This decomposition is linked to a particular and natural “representation...





