Reasoning by induction
The argument by induction is perhaps the most emblematic of mathematical science and the one that fascinates and disconcerts the most.
It is used when one seeks to prove a property ![]() (which depends) on the natural numbers, in other words a statement of the form “
(which depends) on the natural numbers, in other words a statement of the form “![]() “.
“.
Such a statement often covers many other relationships between related objects other than the natural numbers, implicit in the formula ![]() .
.
Reasoning by induction consists in proving ![]() , i.e. the property
, i.e. the property ![]() for the value
for the value ![]() (which is called the induction start), and assuming that
(which is called the induction start), and assuming that ![]() is true (which is called the induction hypothesis), in proving that
is true (which is called the induction hypothesis), in proving that ![]() is true: this is called the induction step. From “close to close”, this leads to the fact that
is true: this is called the induction step. From “close to close”, this leads to the fact that ![]() is true for any natural number
is true for any natural number ![]() .
.
We reason in this way because the set ![]() being infinite, it is not possible to prove the property
being infinite, it is not possible to prove the property ![]() for all the natural numbers
for all the natural numbers ![]() individually, i.e.
individually, i.e. ![]() ,
, ![]() ,
, ![]() , … .
, … .
Example 1
The clause ![]() : “
: “![]() “, where
“, where ![]() denotes a generic natural number, is a property of
denotes a generic natural number, is a property of ![]() which mentions generic real numbers.
which mentions generic real numbers.
- The property
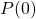 is “
is “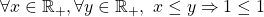 “, since
“, since 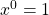 for any real number
for any real number 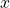
- The induction step consists in proving
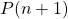 , i.e. “
, i.e. “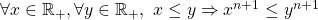 “, by assuming
“, by assuming 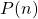 .
. 
Intuitively, we can compare reasoning by induction to a game of dominoes: we have to make the first domino fall, then each time a domino falls, it drags in its fall the following domino and, step by step, all the dominoes fall.
Similarly, you have to prove the property for the first natural number, and then from one step to the next, each time it is proved for one natural number, it will be true for the next number, if at least you can show the transition from one step to the next, which is often the effort involved in the demonstration.
What makes this possible is that one does not demonstrate each step of the induction individually, but “generically”.
Example 2
Using the same example, let us prove by induction on ![]() that for all
that for all ![]() ,
, ![]() is true. Let
is true. Let ![]() be two positive real numbers:
be two positive real numbers:
- Induction start: If
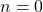 , then
, then 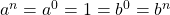 by convention, so the inequality holds for
by convention, so the inequality holds for 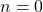
- Induction hypothesis: Suppose that
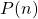 is true for a natural number
is true for a natural number 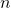 , i.e. that
, i.e. that 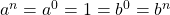
- Induction step: We then have
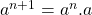 (by definition)
(by definition) 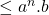 (because
(because 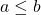 and
and  )
) 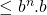 (by applying the induction hypothesis and multiplication by
(by applying the induction hypothesis and multiplication by 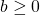 )
) 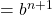
- The property is verified at rank
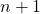 , so we have proved by induction that it is verified for all
, so we have proved by induction that it is verified for all 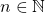 .
. 
The justification of this type of argument is based on the induction principle. Indeed, to show that the property ![]() is true for any natural number
is true for any natural number ![]() is to prove that the set
is to prove that the set ![]() of natural numbers for which
of natural numbers for which ![]() is true (symbolically
is true (symbolically ![]() ), is the set whole set
), is the set whole set ![]() .
.
For that, one applies the induction principle (REF): one must show that ![]() (in other words that the property
(in other words that the property ![]() is true, initial step), then that
is true, initial step), then that ![]() as soon as
as soon as ![]() (in other words, that
(in other words, that ![]() is true as soon as
is true as soon as ![]() is true, induction step). The principle of demonstration by induction is thus a reformulation of the induction principle!
is true, induction step). The principle of demonstration by induction is thus a reformulation of the induction principle!