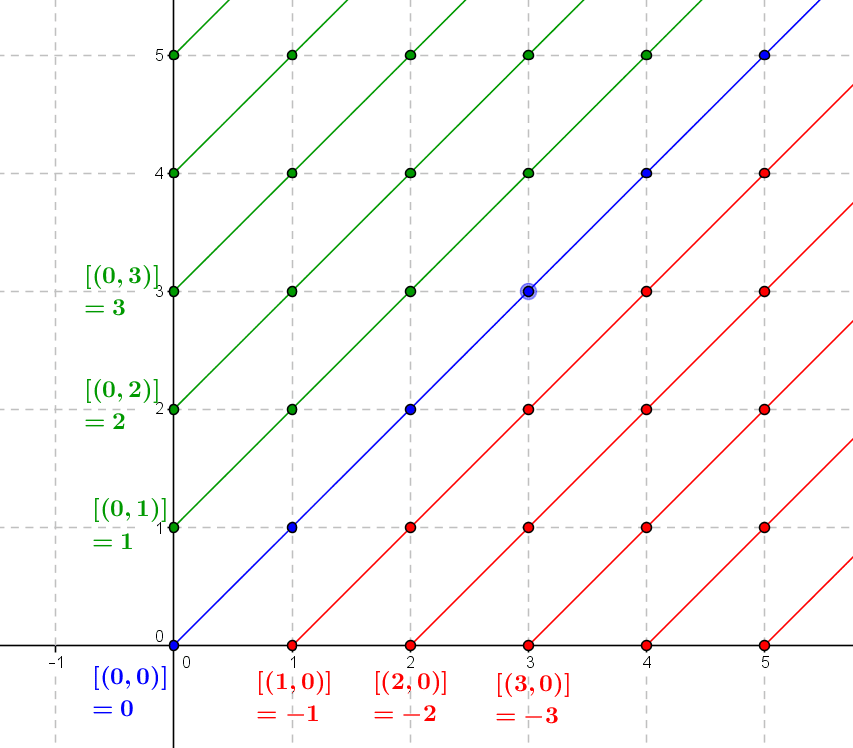
by M4t_6_onL | Jul 30, 2021 | Number theory, Set theory
Integers are an extension of the natural numbers where the existence of subtraction provides a more appropriate framework for certain questions of arithmetic. They can be described axiomatically, but can also be constructed from the set of natural numbers and some...
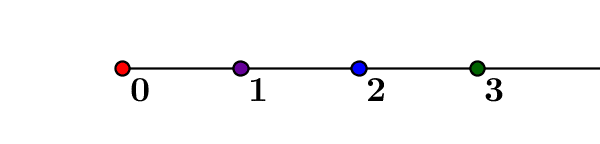
by M4t_6_onL | Jul 30, 2021 | Number theory, Set theory
Mathematical science does not seek to define the notion of a natural number, but to understand the set of natural numbers. “Natural numbers have been made by God, everything else is the work of men”. Leopold Kronecker 1.We don’t define the natural...
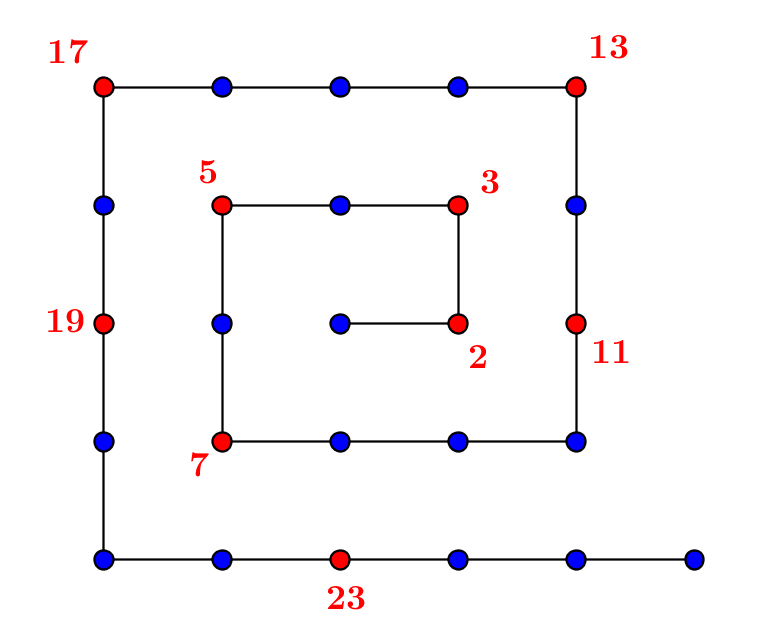
by M4t_6_onL | Jul 17, 2021 | Number theory, Set theory
The prime natural numbers are those which have no divisors other than 1 and themselves. They exist in infinite number by Euclid’s theorem, which is not difficult to prove. 1.Prime numbers 1.1.Divisors and primes A prime number is a non-zero natural number (see...
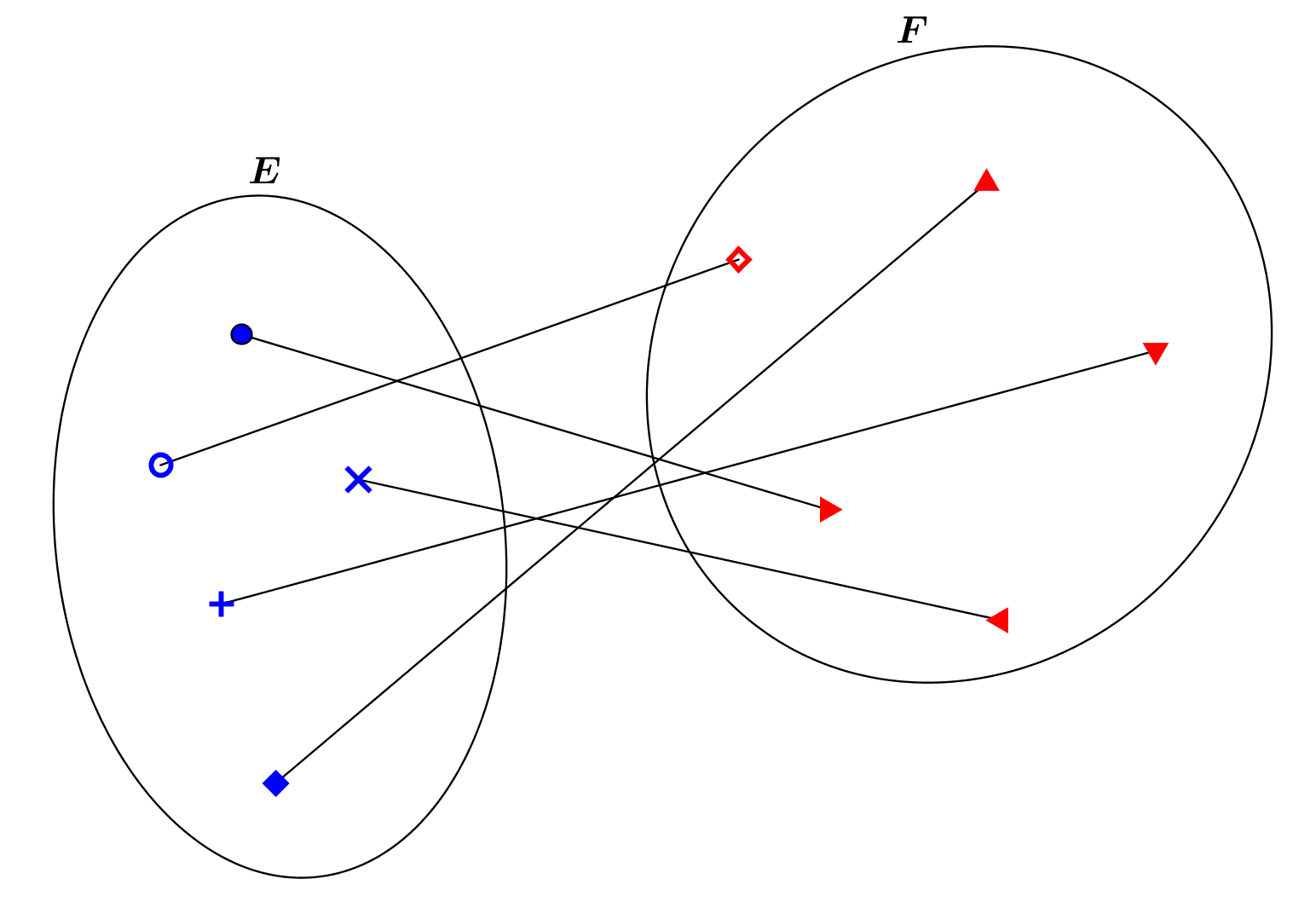
by M4t_6_onL | Jul 17, 2021 | Functions, Set theory
A finite set is a set that can be counted using the natural numbers \(1,\ldots,n\) for a certain natural number \(n\). But what is counting ? And then, what is an infinite set? 1.Comparing sets : the notion of bijection The notions of finite set and infinite set, and...
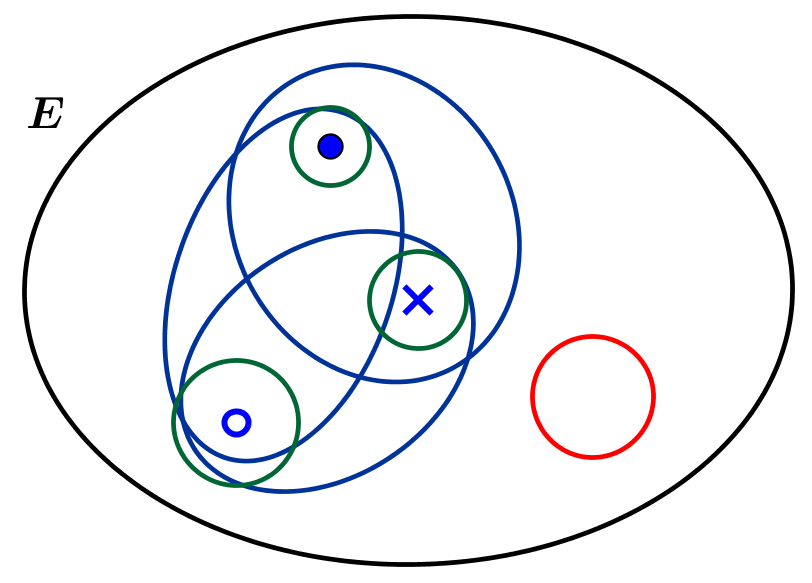
by M4t_6_onL | Jul 2, 2021 | Set theory
Naive set theory or “potato science” is the natural (and understandable!) foundation of mathematical science. “I know what time is. If you ask me, I don’t know anymore.” Augustine. This insightful quote from Augustine emphasises that...





