There are various ways of defining complex numbers. The most direct way is to look at them as points or vectors of the Euclidean plane. Addition and multiplication are then defined using the coordinates.

1. The set \(\mathbb C\) of complex numbers

1.1. A complex number is a two-dimensional number

A complex number is simply a vector or point of the Euclidean plane \(\mathbb R^2=\mathbb R\times \mathbb R\) (see The Euclidean Plane). In other words, it is a pair \((a,b)\) of real numbers, i.e. a “two dimensional” number. When we consider it as a complex number, it is because we implicitly consider it as integrated to a particular algebraic structure on \(\mathbb R^2\).

1.2. The addition and multiplication of complex numbers

Let us be more precise: this “structure” consists of vector addition and complex (i.e. geometric) multiplication. For vector addition, if \((a,b)\) and \((c,d)\) are two vectors of the plane \(\mathbb R^2\), then by definition they are added “coordinate-by-coordinate”, i.e. \((a,b)+(c,d)=(a+c,b+d)\). As for complex multiplication, instead of multiplying “coordinate-by-coordinate”, we multiply as follows: \((a,b).(c,d)=(ac-bd,ad+bc)\). This multiplication corresponds geometrically to what is called a plane similarity (defined by the number \((a,b)\) and applied to the number \((c,d)\)), which is a transformation of the plane preserving the “shape” of the objects (hence the term “similarity”, from the adjective “similar”). As in the set of real numbers, addition and multiplication are associative and commutative (they can be done in any order). Also, multiplication is distributive over addition : if \((a,b), (c,d)\) and \((e,f)\) are complex numbers, we have \((a,b).((c,d)+(e,f))=(a,b).(c,d)+(a,b).(e,f)\), which can be checked from the definition.

1.3. The “field” of complex numbers

In learned terms, we say that we do not consider only on \(\mathbb R^2\) the “product vector space” structure, nor the “product ring” structure, but a “ring structure” which we note \(\mathbb C\). The “zero” for the addition is the number \((0,0)\) (geometric origin of the plane), since \((a,b)+(0,0)=(a,b)\) for any complex number \((a,b)\in\mathbb C\). The “one” for the multiplication is the number \((1,0)\), since \((a,b).(1,0)=(a.1-0.0,a.0+b.1)=(a,b)\) by definition. This structure is what is called a field: every non-zero element has an inverse, which can be seen as follows. If \((a,b)\in\mathbb C\) is non-zero, then either \(a\neq 0\) or \(b\neq 0\) and in both cases, we have \(a^2+b^2\neq 0\), and then \((a,b). (\dfrac{a}{a^2+b^2},-\dfrac{b}{a^2+b^2})=(\dfrac{a^2+b^2}{a^2+b^2},\dfrac{-ab+ba}{a^2+b^2})=(1,0)\), so that \((\dfrac{a}{a^2+b^2},-\dfrac{b}{a^2+b^2})\) is the inverse of \((a,b)\)!

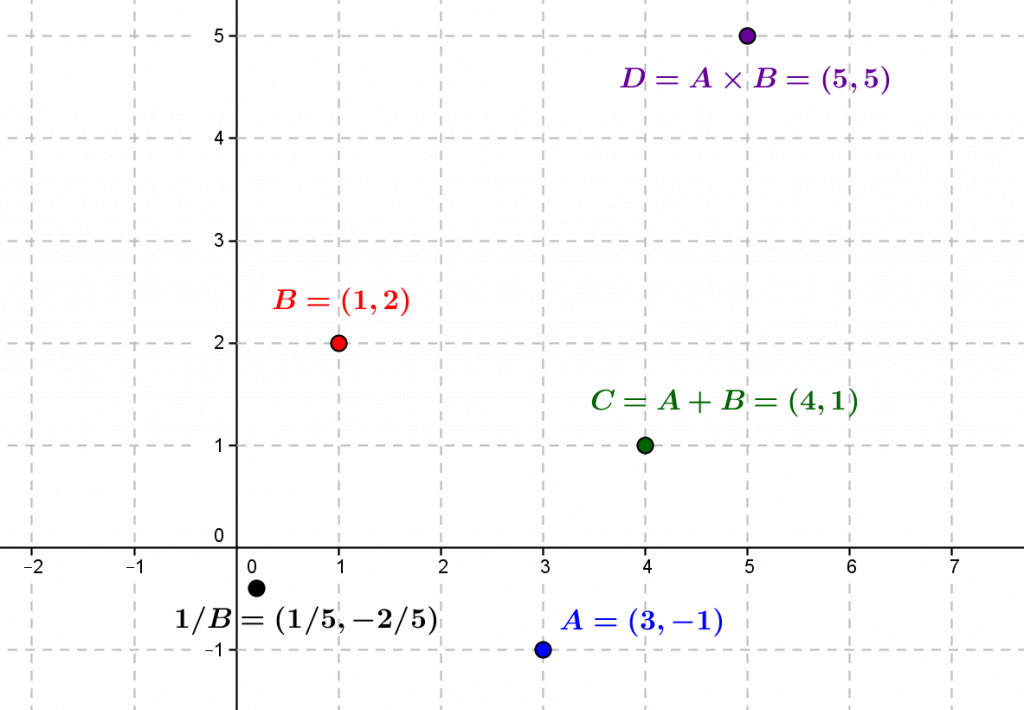
In the following figure, we have represented two points in the plane, \(A\) and \(B\), considered as complex numbers, as well as their sum \(C=A+B\) and their (complex) product \(D=A\times B\). The point \(1/B\) is the complex inverse of \(B\).

2. Real part and imaginary parts

2.1. An imaginary square root of $-1$

In order to explain what they are, we did not introduce the complex numbers with their usual notation, which we now introduce with an algebraic justification. A particularity of these numbers is that there is a complex number $(a,b)$ such that $(a,b)^2=-1$ (!), in other words a “square root of $-1$”. When we write this, we have identified the (real) number $-1$ with the complex number $(-1,0)$: we are in fact identifying each real number $a$ with the complex number $(a,0)$. We say that we have a field homomorphism from $\mathbb R$ into $\mathbb C$ and geometrically, this amounts to considering the “real line” $\mathbb R$ (see What is a real number?) as the abscissa axis. The “square root” $(0,1)$ of $-1$ is then “outside” the set $$mathbb R$, it is said to be “imaginary” !

2.2. The usual notation of complex numbers

There are in fact two complex numbers which square $-1$, the number $(0,1)$ and the number $(0,-1)$, which can be checked for example for the first one by calculating $$(0,1)^2=(0,1).(0,1)=(0.0-1.1,0.1+1.0)=(-1,0). $$ The complex number $(0,1)$ is denoted $i$, and because of this algebraic property it is much more convenient, both algebraically and geometrically, to write a complex number of the form $(a,b)$ in the form $a+ib$, which is the notation $a.1 +b.i=a.(1,0)+b.(0,1)$. Indeed, we can multiply any complex number $(a,b)$ by a real number $c$ given as follows, considering it as a vector: $c.(a,b)=(ca,cb)$. It follows that the vector $a+ib=a.1+b.i$ is exactly $a.(1,0)+b.(0,1)$ by the identification of real numbers, or $(a,0)+(0,b)=(a,b)$.

2.3. Real part, imaginary part, affix

In this way, the description of the multiplication of complex numbers is conveniently found, thanks to the properties of the particular number $i$. If $(a,b)$ and $(c,d)$ are two complex numbers, which we now note $a+ib$ and $c+id$, we can indeed calculate directly, with the usual rules of $+$ and $\times$, $$\begin{eqnarray} (a+ib). (c+id)&=& ac+(ad).i+(bc).i+(bd).i^2\nonumber\\ &=& ac+(ad+bc).i+(bd).(-1)\nonumber\\&=&(ac-bd)+i(ad+bc) !\end{eqnarray}$$ The important thing here is to distinguish between vector multiplication and complex multiplication and to understand where real numbers are identified with their corresponding complex number. The real number $a$ is called the real part, and the real number $b$ the imaginary part of the complex number $a+ib$. These two real numbers are the coordinates of this number as an element of $\mathbb R^2$, and the complex number $z=a+ib$ is called the affix of the point $(a,b)$. In a sense it is a “complex coordinate”.

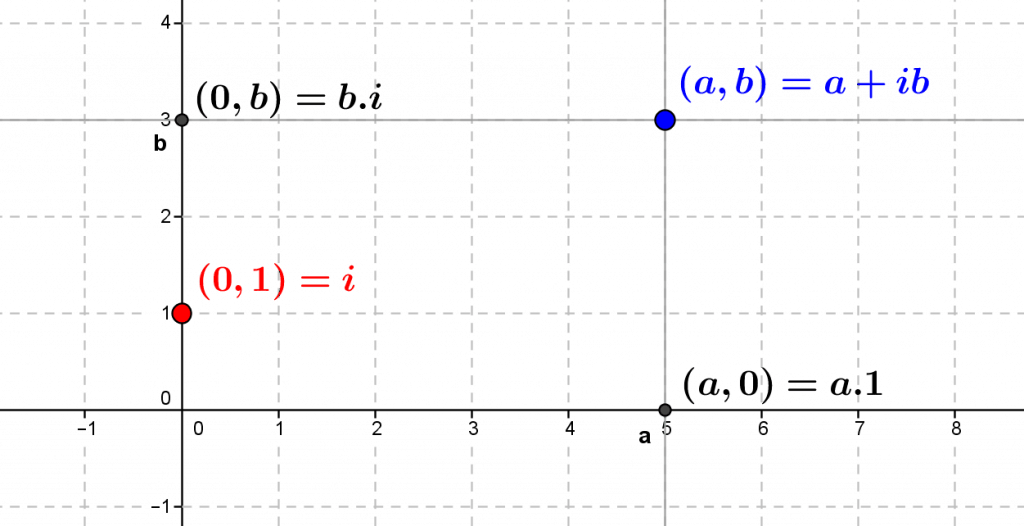
On the following figure, we have represented the complex number $a+ib=(a,b)=(5,3)$, with its two co-ordinates $a$ and $b$, the corresponding complex numbers (projections on the axes), and the number $i$. $5$ is the real part, $3$ is the imaginary part, of this complex number $5+3i$, affix of the point $(5,3)$.

3. Conjugate and module of a complex number

3.1. Conjugate and real and imaginary parts

The complex number $z=a+ib$ being the point $(a,b)$ of the Euclidean plane, its symmetrical with respect to the x-axis is the point $(a,-b)$, that is to say the complex number $a-ib$. This number is denoted $\overline z$ and is called the conjugate of $z$. The conjugate of a complex number has several interesting properties and plays an essential role in the whole theory of these numbers. For example, it allows us to recover the real and imaginary parts of the number $z$, since by writing $z+\overline z=(a+ib)+(a-ib)=2a$ we see that $Re(z)=\dfrac{z+\overline z}{2}$. Similarly, writing $z-\overline z=(a+ib)-(a-ib)=2ib$, we get $Im(z)=\dfrac{z-\overline z}{2i}$, since we can divide by the complex number $2i$ which is non-zero.

3.2. Conjugation and structure

We have seen that a real number $x$ can be identified with the complex number $x+0i$, so that a complex number $z=a+ib$ “is” a real number exactly when its imaginary part is zero – i.e. $Im(z)=0$, or when it is equal to its real part – i.e. $z=Re(z)$. This can be rephrased from the conjugate by simply saying that $z$ is real if and only if $z=\overline z$. Geometrically, this corresponds to the situation where $z$ is its own symmetric about the x-axis. In particular, any real number is equal to its own conjugate. Moreover, if $z$ and $w$ are two complex numbers, it is easy to show from the definition that $\overline {z+w}=\overline z+\overline w$ and that $\overline{z\times w}=\overline z\times \overline w$. In other words, the conjugation operation “preserves” the operational structure of the complex numbers, we say that it is an automorphism of the body $\mathbb C$.

3.3. Module of a complex number

The module of a complex number $z=a+ib$ is its (Euclidean) norm as a vector, i.e. its Euclidean distance to the origin as a point. In other words, it is the non-negative real number denoted $|z|$ (as the absolute value) and defined by $|z|=sqrt{a^2+b^2}$. The module of complex numbers extends the absolute value of real numbers, in the sense that if $x$ is a real number conceived as the complex number $x+0i$, its module as a complex number is its absolute value as a real number (since $|x|=\sqrt{x^2}=\sqrt{x^2+0^2}$). Here again, the module can be described from the conjugate: since $i^2=-1$ by definition of $i$, we can indeed write $a^2+b^2$ as a remarkable identity of the form $a^2-c^2$, with $c=ib$! This means that $a^2+b^2=a^2-(ib)^2=(a+ib).(a-ib)=z.\overline z$, and thus that $|z|=sqrt{z.\overline z}$. In particular, if $z=a+ib$ is not zero, we have a convenient formula for calculating its inverse: since $|z|\neq 0$, we have $\dfrac{z.\overline z}{|z|^2}=1$, so that $$\dfrac{1}{z}=\dfrac{\overline z}{|z|^2}=\dfrac{a-ib}{a^2+b^2}.$$
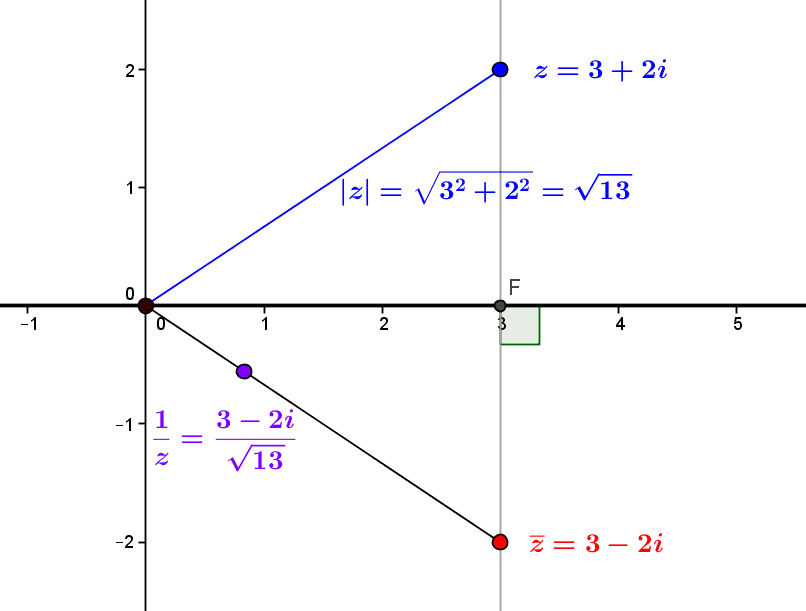
In the following figure, we have represented the complex number $z=3+2i$ and its conjugate $\overline z=3-2i$, symmetrical to $z$ about the x-axis (in black). The module of $z$ is $\sqrt{13}$, which makes it possible to calculate and locate its inverse $1/z=\dfrac{3-2i}{13}$ (in purple).

4. Other definitions of complex numbers…

Finally, let us mention that there are other constructions of the set $\mathbb C$ (rather the “structure” $\mathbb C$) of complex numbers, in the sense that they give essentially the same mathematical object. For example, it is possible to divide polynomials with real coefficients (algebraic expressions of the form $a_0+a_1x+\ldots+a_nx^n$, with the $a_i$ of the real numbers) as one divides integers. Then the set of remainders of the Euclidean division of these polynomials by the polynomial $x^2+1$ (for example) gives another version of the set $\mathbb C$, where in this case $i$ is the polynomial $x$ !

Conclusion: a complex number is a “two-dimensional” number, implicitly conceived as part of a structure with a particular vector addition and geometric multiplication.