Russell’s paradox or antinomy is a very simple paradox in naive set theory, which arises when one tries to define a “set of all sets”. Its resolution relies on the introduction of the notion of class and the distinction of sets among classes. Thanks to class theory, it is then possible to transfigure naive set theory through the theory of ordinals and cardinals.

1.Russell’s paradox or antinomy

1.1.The set of all sets

Russell’s paradox, named after the British philosopher, mathematician and logician Bertrand Russell, shows the logical limits of using the concept of set too broadly in naive set theory. This paradox appears when we consider the possibility of a “set of all sets“.

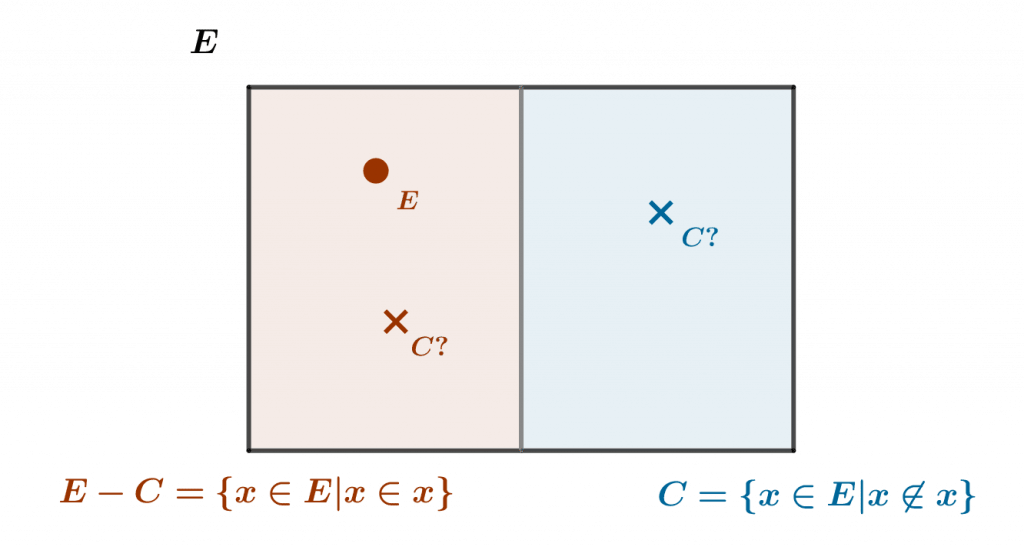
It all starts from the following simple observation: if such a set $E$ exists, i.e. is allowed in the theory, then it is necessarily, as a set, an element of itself.

1.2 The subset of sets that do not belong to themselves

This property is rather counter-intuitive: we generally distinguish a set from the elements it contains, and set theory is in a way designed for this. However, it does not appear contradictory as such. But among sets, we could consider only those which are not elements of themselves.

This property is quite unambiguous in naive set theory, and thus allows, since we have supposed the existence of $E$, to define the subset $C$ of $E$ formed of all the sets which do not belong to themselves, symbolically $C=\{x\in E : x\notin x\}$.

1.3 Formulation of the paradox

We then ask the following question: is the set $C$ a member of itself? Since natural mathematical logic is considered here as “classical”, the principle of the excluded middle is valid: either this statement is true, or its negation is true. Let us first suppose that $C$ is an element of itself, in other words that $C\in C$ : as $C\in E$, by definition of $C$ we deduce that $C\notin C$, which contradicts the hypothesis.

Suppose then that $C\notin C$ : we must deduce, by definition of $C$, that $C\in C$, which again contradicts the hypothesis ! Thus, neither of the two alternatives imposed by the principle of the excluded middle, namely that $C\in C$ or $C\notin C$, can be true, which contradicts natural mathematical logic. This is a version of the so-called Russell paradox.

2. Solving the paradox by means of class theory

2.1.Distinguishing sets from classes

In general, in the presence of a paradox, i.e. an “apparent contradiction”, one seeks an explanation and a resolution. In the present case, what is also called “Russell’s antinomy” can be solved by introducing into naive set theory a distinction between sets and classes.

This distinction is made in the following way. The notion of set in the basic theory is replaced by the notion of class, which will play the same role. It must then be decreed that only certain classes are what we intuitively consider to be sets, by defining these precisely as classes that can be elements of another class (an idea from Kurt Gödel). A class which is not a set (and therefore not an element of any class!) is then called a proper class.

2.2.The proper class of all sets

Thus, by forming the class $C$ of all sets in this sense, and by also specifying that no class can be an element of itself as a new axiom or principle of the theory, we explicitly avoid that $C$ is itself a set, and thus Russell’s paradox.

It is thus a proper class and in this situation, as it has been excluded that no class can belong to itself, the class $C$ is in fact also, trivially, the class of all sets which do not belong to themselves.

3.Other interesting classes

This simple approach allows naive set theory to be completely transfigured (without the need, as is often mistakenly believed, for a formal axiomatic theory). Indeed, the possibility to distinguish sets from proper classes allows to gather certain sets into classes, which themselves allow to develop set theory in a much more advanced way. We will mention two of them here, the class of ordinals and the class of cardinals.

3.1.The proper class of ordinal numbers

Perhaps the most suggestive example is the class of ordinals. Ordinal numbers are “formal numbers”, i.e. sets, allowing to enumerate any set, finite or infinite. Thanks to the class theory, we can then form the class $Ord$ of all ordinals, which would not be possible without the distinction between sets and classes. Indeed, if we were to define a “set of all ordinals” we would end up in a situation where this set itself would be, by definition, an ordinal, a situation generating another form of paradox (for example, Burali-Forti paradox). Distinguishing such a class, on the other hand, makes it possible to avoid this type of problem and to reason by “transfinite recursion“, i.e. using arguments analogous to reasoning by induction, but concerning all ordinal numbers, finite or infinite!

3.2 The subclass of cardinal numbers

Among the ordinals, we also distinguish the cardinals or cardinal numbers, which are the ordinals that allow us to count any set. The cardinals constituting a sub-class $Card$ of the class $Ord$ of ordinals, it is then possible to assign thanks to the axiom of choice a single cardinal number to any set, and to develop a so-called “transfinite”, i.e. infinite, arithmetic, and thus to compute with infinite quantities! This is not possible with a naive set theory which does not distinguish between sets and classes. Here again, if we simply tried to define a “set of all cardinals”, we would end up with a paradox, known as Cantor’s paradox.

Conclusion

Russell’s paradox, as well as other paradoxes, arise when one adopts too “naive” an approach to set theory. By introducing an elementary distinction between classes and sets, one resolves Russell’s paradox and other historical paradoxes, and ends up with a sound set theory without logical formalism.