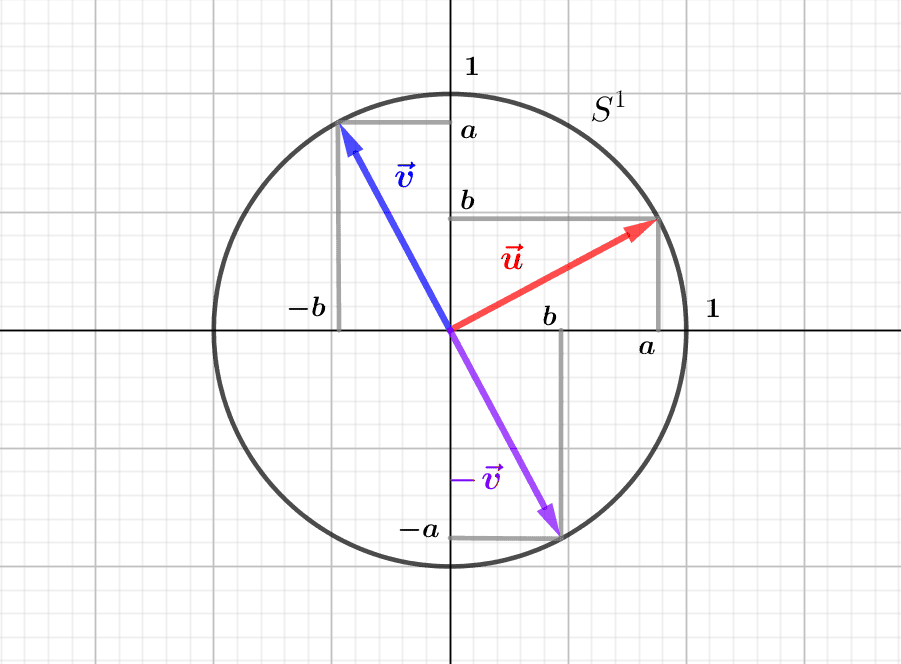
by M4t_6_onL | Apr 28, 2022 | Algebra, Geometry
The linear transformations of the Euclidean plane are the invertible linear applications, i.e. of non-zero determinant. They allow us to move from one basis of the plane to another, and the orthogonal transformations, i.e. the vectorial isometries, exchange the...
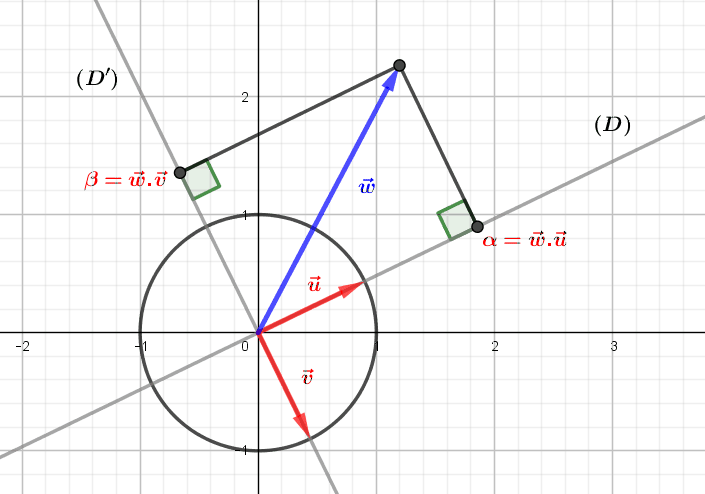
by M4t_6_onL | Apr 23, 2022 | Algebra, Geometry
The representation of the Euclidean plane as the Cartesian product \(\mathbb R^2\) allows us to decompose any vector of the plane into two coordinates, its abscissa and its ordinate. This decomposition is linked to a particular and natural “representation...




