The real numbers are all the “quantities” that we can order, and we can “construct” them in various ways thanks to set theory.
“Numbers govern the world.” Pythagoras
The real numbers idealise all the “points” of the geometrical line, or from the arithmetic point of view all the possible “measures” of magnitude. The Ancients knew thanks to Pythagoras’ theorem that one could not measure the diagonal of the square of side 1 by a rational number, i.e. fractional, of the form \(\dfrac a b\) for integers \(a\) and \(b\) (one says that this diagonal is incommensurable). Today, we would say that the length of this diagonal is \(\sqrt 2\).
A host of “quantities” have since been discovered that are not rational numbers, such as \(\pi\), the ratio of the perimeter of a circle to its diameter, or \(e\), the basis of the exponential function. Real numbers theorise all those quantities that can be “ordered”, like rational numbers, but which exceed them, as it were. They can be constructed in a precise mathematical sense, from rational numbers, in several ways: the most famous are undoubtedly the method of Cauchy sequences, and that of Dedekind cuts.
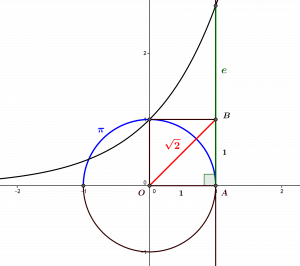
The diagonal of the square of side \(1\) is “incommensurable”: by Pythagoras’ theorem, we have \(OA^2+AB^2=OB^2\), so that \(OB^2=2\); yet, it can be shown that there is no rational number \(r\) which square is equal to \(2\), so that the length \(OB\) cannot be a rational number. Some famous real numbers, such as \(\pi\) and \(e\), are also represented.
1.There are “holes” in the set of rational numbers
1.1.The problem with the axiomatisation of the continuum
As we saw with the natural numbers (see What is a natural number?), in order to theorise a type of mathematical object we are interested in the set of objects of this type, of which we try to identify the fundamental properties (“postulates” or “axioms”). It is the same for real numbers: even if the intuition of what they are is more or less accessible to us, the mathematical theory about them will consist in describing a set, noted \(\mathbb R\), of real numbers.
Contrary to the case of the natural numbers, however, it is not obvious to give elementary intuitive properties which would describe this set by clearly differentiating it from the set \(\mathbb Q\) of rational numbers. For example, the idea of “continuity” of a geometrical line can be expressed by saying that for two points A and B of this line, there always exists a point C strictly comprised between A and B: one can “fill” indefinitely the spaces determined by two points. Now, this property is already verified for rational numbers: if \(x,y\) are such numbers, with \(x<y\), we can easily show that there always exists a rational number between the two, that is to say a rational number \(z\) such that \(x<z\) and \(z<y\) (for example, \(z=\dfrac{x+y}{2}\)).
This property of the set \(\mathbb Q\) has caused this set to be called in the past the “first order continuum” (see for example Henri Poincaré, in “La science et l’hypothèse”). The idea is to differentiate this continuum from a “second order” continuum, which would correspond precisely to the set \(\mathbb R\) of real numbers. This also means that this first idea does not work to identify the set \(\mathbb Q\).
1.2.Some quantities of geometry are not measurable by rational numbers
Let us return to the example of the length of the diagonal of the square of side \(1\): this length is \(\sqrt 2\), a number which can be shown not to be rational, which Pythagoras already knew and which was at the time a tragedy for his philosophy, because certain geometrical relations did not correspond to known numbers! On the other hand, this number is a solution of the equation \(x^2-2=0\), since by definition the square of \(\sqrt 2\) is \(2\).
There are therefore equations with integer or rational coefficients, which have no solution in \(\mathbb Q\): we expect some of these solutions to be real numbers, as is the case for \(\sqrt 2\): we can indeed place \(\sqrt 2\) on the scale of magnitudes. Other numbers, such as \(\pi\) and \(e\), must also represent quantities, but are not even solutions of an equation. In any case, there are “holes” in the set \(\mathbb Q\), in the sense that some numbers are “missing” to measure certain magnitudes, i.e. certain “numbers” that can be situated in relation to all rational numbers.
It is to the French mathematician Augustin Louis Cauchy that we attribute a construction, perhaps the most famous, of the real numbers from the rational numbers, that is to say a description using the set \(\mathbb Q\) and the resources of naive set theory (see the What is a set?). This construction, like that of the German mathematician Richard Dedekind, exploits this idea of “holes” in the set \(\mathbb Q\).
2.Filling the holes with Cauchy : building the real numbers
2.1.Sequences of rational numbers “as close as we want”
The idea of the Cauchy construction is to consider that the “holes” existing in the set \(\mathbb Q\) can be “approximated” indefinitely by sequences of rational numbers, i.e. infinite lists of numbers \(r_0,r_1,\ldots,r_n,\ldots\), indexed by the natural numbers. There are indeed sequences of rational numbers which have a limit, i.e. which “approach indefinitely” a certain rational number \(r\), in the precise mathematical sense that one can “approach as much as one wants the number \(r\)” provided that one “places oneself far enough in the sequence”; this idea finds a rigorous mathematical formulation thanks to set theory.
For example, the sequence \(1, \frac 1 2, \frac 1 3, \ldots,\frac 1 n,\ldots\) has for limit the number \(0\). Now, it turns out that these sequences, which are called convergent, have another analogous property: their terms are “as close to each other as we want” provided we choose them “far enough in the sequence”. This property, known as “Cauchy’s property” can also be formulated in a rigorous way, and if one notes the obvious analogy with the property of being a convergent sequence, this one is an intrinsic property of the sequence, not calling upon a possible “external” number.
2.2.Filling the “holes” with Cauchy sequences
Now, if all convergent sequences, i.e. which have a limit in the set \(\mathbb Q\), have Cauchy’s property, the opposite is not always true : there are Cauchy sequences of rational numbers, which do not have a limit in \(\mathbb Q\) ! The ingenuity of the Cauchy construction consists in considering that the “holes” of the set \(\mathbb Q\) correspond to virtual limits of Cauchy sequences which do not have any… In other words, we can “represent” what we mean by a “real number” as a limit of such a Cauchy sequence, whether it exists or not.
Strictly speaking, several Cauchy sequences can intuitively determine the same virtual limit, when their respective terms are indefinitely close to each other, in other words when the difference of their respective terms has limit \(0\): we say that two such sequences are equivalent. Thus, we can construct the real numbers as sets of equivalent Cauchy sequences, with the sole resources of set theory (and that of rational numbers, which is based on the theory of natural numbers).
2.3.One extends the “structure” of the set \(\mathbb Q\) to a set \(\mathbb R\) of real numbers}
In this approach, one can represent each rational number \(r\) as a real number: one represents it as the set of sequences equivalent to the constant sequence \(r,r,\ldots,r,\ldots\)! Thus, we can consider that the set noted \(\mathbb R\) of real numbers is an “extension” of the set \(\mathbb Q\) of rational numbers. The arithmetical operations \(+\) and \(\times\) of the rational numbers extend to the set \(\mathbb R\), as well as the order relation \(<\) between the rational numbers, as well as several other properties. The demonstration of these facts is beyond the scope of this article.
The set \(\mathbb R\) has in addition a fundamental property that the set \(\mathbb Q\) already has, called Archimedes’ property: if \(x\) is a real number, there always exists a natural number \(n\) greater than \(x\), i.e. having the property that \(x<n\); this seemingly simple property is essential to real analysis, i.e. the study of functions of real numbers (polynomial functions, roots, sine, cosine, exponential, logarithm. …), as well as the property known as the “upper bound property”, which is not true in the set \(\mathbb Q\) : any subset \(E\) of the set \(\mathbb R\), non-empty and having an upper bound (i.e. such that any element of \(E\) is lower than a certain real number), has an least upper bound, i.e. one which is smaller than any other. This property is analogous to an essential property of the set \(\mathbb N\) of natural numbers: any non-empty subset of \(\mathbb N\) has a smallest element.

A.L. Cauchy
3.The real line is complete: there are no more holes
3.1.All Cauchy sequences of real numbers have a limit
Let us remark about Cauchy’s construction that since we have constructed the set \(\mathbb R\) (also called “real line” because of its geometrical representation) by ” filling the holes ” of the set \(\mathbb Q\), we could ask ourselves if we have filled “all the holes”. In other words, what guarantees us that there are no holes left in \(\mathbb R\), in the same sense that there were in \(\mathbb Q\) ? This question is reformulated with the concepts evoked previously in a precise way: whereas any Cauchy sequence of rational numbers does not have a rational limit, does any Cauchy sequence of real numbers have a real limit? If the answer is negative, we have only moved the problem. Fortunately, the answer is yes, and the proof relies on what is generally called a “diagonal argument”. This property is called the completeness of the real line, the least upper bound property can be deduced from it, and the abstract completeness property gives rise to the theory of spaces with similar properties to this line, called “complete metric spaces”.
3.2.The completeness of \(\mathbb R\) allows the definition of the functions of analysis
This completeness property allows the definition and study of many real functions, such as trigonometric functions (sine, cosine, tangent…) and their reciprocals, polynomial functions, power and root functions, exponential and logarithmic functions…, the knowledge of which is important both for mathematical science itself and for applications of analysis and geometry to other sciences. For example, as we have already discussed the integer \( 2 \) has no square root in the set \(\mathbb Q\). In contrast, any real number \(x\) has a root of any order \(n\) (for a given natural number \(n\)) if \(x\geq 0\), and of any odd order if \(x<0\). Such a root is a real number \(y\) such that \(y^n=x\), and this notion can be defined thanks to the least upper bound property, which follows from the completeness of \(\mathbb R\).
3.3.The quantities of geometry, classical and modern, are measurable by real numbers
On this subject, on the level of the relation between arithmetic and geometry let us note that the new properties of the real numbers make it possible to solve the antique problem of the measurement of the diagonal of the unit square thanks to the number \(\sqrt 2\), but also to measure the diagonal of any rectangle, and the circumference of an unspecified circle thanks to the number \(\pi\): the application of rational numbers to the measurement of certain ratios of quantities associated with plane figures (constructed for example with a ruler and a compass) finds in the theory of real numbers the basis of a vast extension which concerns the application of the measurement of quantities to any real “shape”, in the plane or in higher dimensions. This is linked to the possibility of integration and differentiation theories, and constitutes an essential progress of modern mathematics compared to ancient mathematics. Differential geometry, a geometric theory classically associated with mechanics and physics in general, is made possible by these theories, and thus essentially by the completeness of the real line.
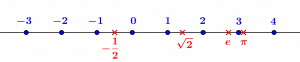
A geometric representation of some real numbers: the integers \(-3,-2,-1,0,1,2,3,4\), the rational number \(-\dfrac{1}{2}\) and the irrational numbers \(\sqrt 2, e\) and \(\pi\), the last two being called “transcendental”.
4.Another way to represent real numbers : Cantor, Dedekind and axioms
4.1.Other ways to fill in the gaps: Cantor and Dedekind’s methods
There are other ways to “construct” a set of real numbers. One of them, that of Georg Cantor, the father of set theory, consists in considering “adjacent” sequences of rational numbers, i.e. sequences varying in opposite directions and approaching each other indefinitely. Another related method, that of Richard Dedekind, consists in considering “cuts” of the set \(\mathbb Q\), that is to say decompositions of this set into a lower part and an upper part. In both cases, the same idea of “filling the holes” is exploited : in the first case, there can be holes between two adjacent sequences, in the second case one can cut the set \(\mathbb Q\) at the level of a “hole” !
4.2.The same essence of a “complete archimedean field”
What is important to remember is that these constructions lead to the same mathematical “object”, in the sense that we mentioned in the article on natural numbers: even if the sets of real numbers “constructed” by these methods are strictly speaking different, they are mathematically indistinguishable. It is moreover remarkable that one can explicitly give an abstract list of axioms which characterise (any version of) the set \(\mathbb R\) ! This is what is cleverly called a complete archimedean field.
4.3.Real numbers in other universes
Finally, let us note that Dedekind’s construction, for example, can be reproduced in certain mathematical universes called “topos” when these possess a “fairly rich structure”. This means that real “numbers” can be defined or constructed in universes other than a universe of sets, using a more demanding logic, called “intuitionistic”, than the usual logic; we then obtain objects of another nature, which are sometimes similar to ” true” real numbers! For example, continuous real functions are real numbers “in another universe”. But this is another story.
R. Dedekind
In short
If the intuition of real quantities exists, and if their quest is born from an observation of the incompleteness of an arithmetical or geometrical situation, discovering that they could be thought of as numbers exceeding but extending the rational numbers was not so obvious. Determining the set of real numbers is not as straightforward as defining the set of natural numbers, but with the resources of integers and set theory, we end up with the unambiguous definition of a formidable and perfectly axiomatised mathematical object, which solves the problem of measuring geometric quantities by numbers that can be ordered in a continuum.

0 Comments