1.The intuition of rational numbers

Rational numbers, i.e. “fractional” numbers, such as \(-\frac 1 2, \frac{27}{4}, \frac{312}{-6783},\ldots\), form an intuitive set which we note \(\mathbb Q\). It is an extension of the set \(\mathbb Z\) of integers (see What is an integer?). To these we have added inverses for multiplication to each non-zero number: in other words, for any integer \(n\neq 0\), a rational number \(\frac 1 n\) such that \(n\times \frac{1}{n}=1\). Any non-zero rational number \(\frac a b\) (i.e., for which \(a \neq 0\) actually has an inverse \(\frac b a\) for multiplication, which makes it possible to divide any rational number \(\frac a b\) by any other non-zero rational number \(\frac c d\): the result is \(\frac a b / \frac c d= \frac{ad}{bc}\).

In the set \(\mathbb Q\) we can extend the usual operations \(+\) and \(\times\) between integers, as well as the relation \(<\) of strict order which allows to compare them. The basic properties of addition and multiplication extend to it, as well as the distributivity property of multiplication over addition: if \(p,q,r\) are three rational numbers, we always have the equality \(p\times (q+r)=p\times q+p\times r\). However, as any rational number is divisible by any non-zero rational number, the questions of arithmetic such as they arise in the set \(\mathbb Z\) no longer arise in the set \(\mathbb Q\) ! But thanks to the possibility of carrying out all the divisions, one can approach these questions differently, in particular via the theory of valuations. Let us note that if certain properties of \(<\) extend from \(\mathbb Z\) to \(\mathbb Q\), in particular its “compatibility” with \(+\) and \(\times\), the natural order between rational numbers possesses the so-called density property. This means that if \(q,r\) are rational numbers with \(q<r\), one can always find a rational number \(s\) such that \(q<s<r\), for example \(\frac{q+r}{2}\), which is obviously not the case in \(\mathbb Z\).

The rational number \(s=-\frac{991}{1887}\), which represents the middle of the segment \([q,r]\), is strictly between the rational numbers \(q=-\frac{-54}{17}\) and \(r=-\frac{236}{111}\).

2.Constructing rational numbers

As we do for the integers from the natural numbers and an equivalence relation, rather than describing the set \(\mathbb Q\) by axioms it is possible to construct this set, this time from the set \(\mathbb Z\) of integers. By analogy with the construction of \(\mathbb Z\) (see What is an integer ?), we represent the rational numbers by pairs of integers. The couple \((a,b)\) represents the “operation” \(a/b\) of division of \(a\) by \(b\). Since we cannot divide by a non-zero number, we must however exclude the case where \(b=0\), so we consider all the pairs \(a,b\) of integers for which \(b\neq 0\), which form a set which is cleverly written \(\mathbb Z\times \mathbb Z^*\).

As with the construction of the set \(\mathbb Z\), several pairs can define the same “division” or the same “fraction”. The calculation on the fractions tells us indeed that the fractions \(\dfrac a b\) and \(\dfrac c d\) are equal when precisely \(a\times d=b\times c\). We must therefore also identify here the pairs which represent the same fraction. Two pairs \(a,b\) and \(c,d\) are said to be equivalent when \(a\times d=b\times c\), and an equivalence class is a set of pairs all equivalent to the same pair. The set \(\mathbb Q\) is then defined as the set of these equivalence classes, which is also called a “quotient of the set \(\mathbb Z\times \mathbb Z^*\)”. The equivalence class of the couple \(a,b\) is then noted \(\dfrac a b\), notation which designates henceforth a set, itself an element of \(\mathbb Q\) such as newly constructed ! It is the rational number defined by the couple \((a,b)\).

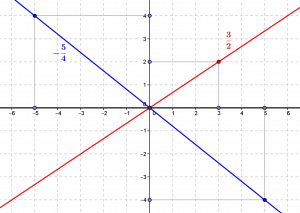
The rational numbers can be represented as lines in the plane passing through the origin and one of the nodes of the plane (points with integer coordinates), except for the line represented by the x-axis (in black). Several nodes of the plane (pairs of equivalent integers) define the same rational number, in particular the opposite points (example of the line in blue).

3.A natural extension of the set \(\mathbb Z\)

Thanks to this representation of the rational numbers, one can consider any integer \(n\) as a fraction, namely \(\frac n 1\), the equivalence class of the couple \((n,1)\). As for the rintegers, the number \(n\) is also represented by the couple \((na,a)\) for any integer \(a\neq 0\).Indeed, by definition, the couples \(n,1)\) and \(na,a)\) are equivalent, since \(n\times a=na\times 1\), which means that their classes are the same, thus that the fractions \(\frac n 1\) and \(\frac{na}{a}\) are equal.

If one considers from now on the set \(\mathbb Q\) as the set of these equivalence classes of pairs of integers, one can extend the addition of the integers by \(\frac a b+\frac c d=\frac{ad+bc}{bd}\) and their multiplication by \(\frac a b\times \frac c d=\frac{ac}{bd}\). The “zero” of addition is the fraction (the class) \(\frac 0 1\), which is equal to \(\frac 0 n\) for all \(n\neq 0\), and the “one” of multiplication is the fraction \(\frac 1 1\), which is equal to \(\frac n n\) for all \(n\neq 0\). The subtraction of two rational numbers is then defined as \(\frac a b – \frac c d= \frac{ad-bc}{bd}\). One can also extend the order between integers by first decreeing that \(\frac a b>0\) if and only if \(\frac a b>0\) and that \(\frac a b<\frac c d\) if and only if \(\frac c d- \frac a b>0\).

4.Recovering the set \(\mathbb Q\)

In this way, the usual basic properties of \(+\), \(\times\) and \(<\) are extended from the set \(\mathbb Z\) to the set \(\mathbb Q\) thus constructed. The interest of the construction appears then in the possibility of finding a multiplicative inverse for any non-zero rational number \(\frac a b\). For such a number, the numerator is not zero, so we can also consider the fraction \(\frac b a\), and by definition of the multiplication we can write \(\frac a b a =\frac{a\times b}{b\times a}= \frac 1 1=1\) in \(\mathbb Q\). One could also demonstrate from the construction all the intuitive particular properties of \(\mathbb Q\).

Finally if we also keep in mind the construction of \(\mathbb Z\) from \(\mathbb N\), with two steps we have constructed the set \(\mathbb Q\) from the set \(\mathbb N\) (add the opposites for addition, then add the inverses for multiplication). One can actually follow these two steps in the other direction. We would start by constructing all fractions of the form \(\frac a b\) for \(a\) and \(b\) natural numbers this time, i.e. doing the same thing as here by replacing \(\mathbb Z\) by \(\mathbb N\). At the end of this first construction one would end up with the set \(\mathbb Q_+\) of positive rational numbers only, and then one would have to add the opposites for the addition as one did for \(\mathbb Z\) from \(\mathbb N\) ! The result would be “formally different” (two different sets as such) but “essentially the same” from the mathematical point of view, i.e. resulting in describing the same “structure” \(\mathbb Q\) of rational numbers.