
par Jean Barbet | Juil 8, 2023 | Ensembles, Logique, Nombres
L’arithmétique naturelle est la science des nombres entiers naturels : elle repose sur l’addition, la multiplication, l’ordre naturel et la divisibilité. Or, toutes ces opérations et relations se définissent à partir de la seule fonction successeur,... 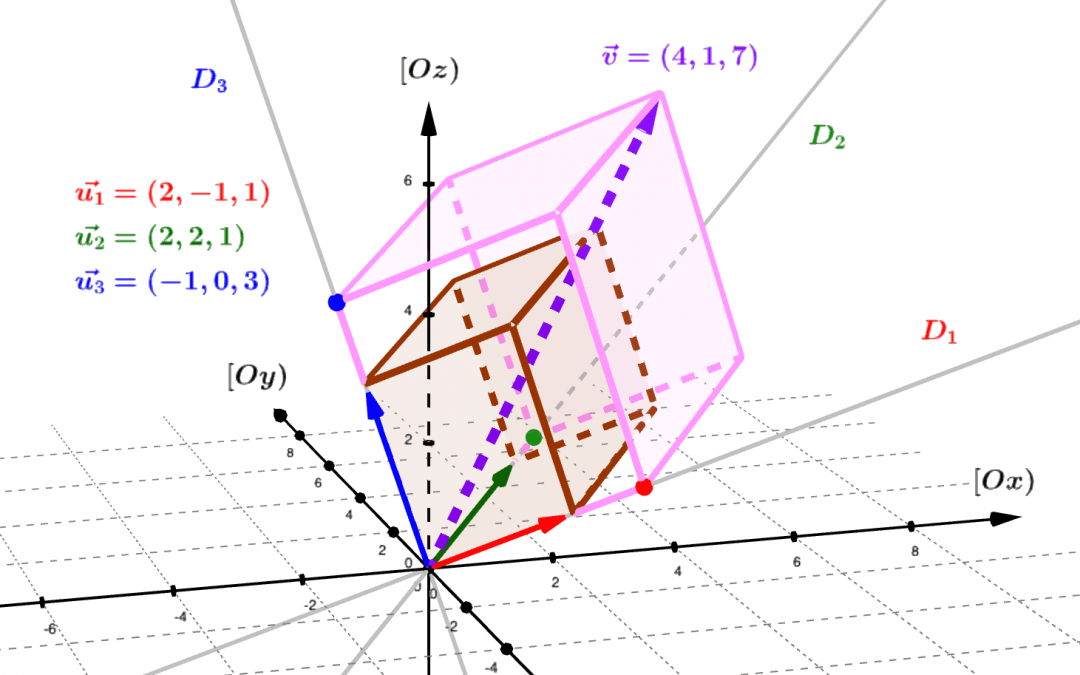
par Jean Barbet | Juil 3, 2023 | Algèbre, Géométrie
Comme dans le plan euclidien $\mathbb R^2$ , il existe dans l’espace euclidien $\mathbb R^3$ une infinité de bases ou « systèmes de représentation » des vecteurs : l’espace étant intuitivement de dimension 3, ces bases sont toujours formées de 3 vecteurs... 
par Jean Barbet | Juin 6, 2023 | Algèbre, Nombres
Les corps finis traduisent sur le plan structurel certaines propriétés arithmétiques et servent de « corps de restes » en théorie des nombres. Par analogie avec les corps $\mathbb R$ des nombres réels et $\mathbb C$ des nombres complexes, le nombre $-1$ peut y... 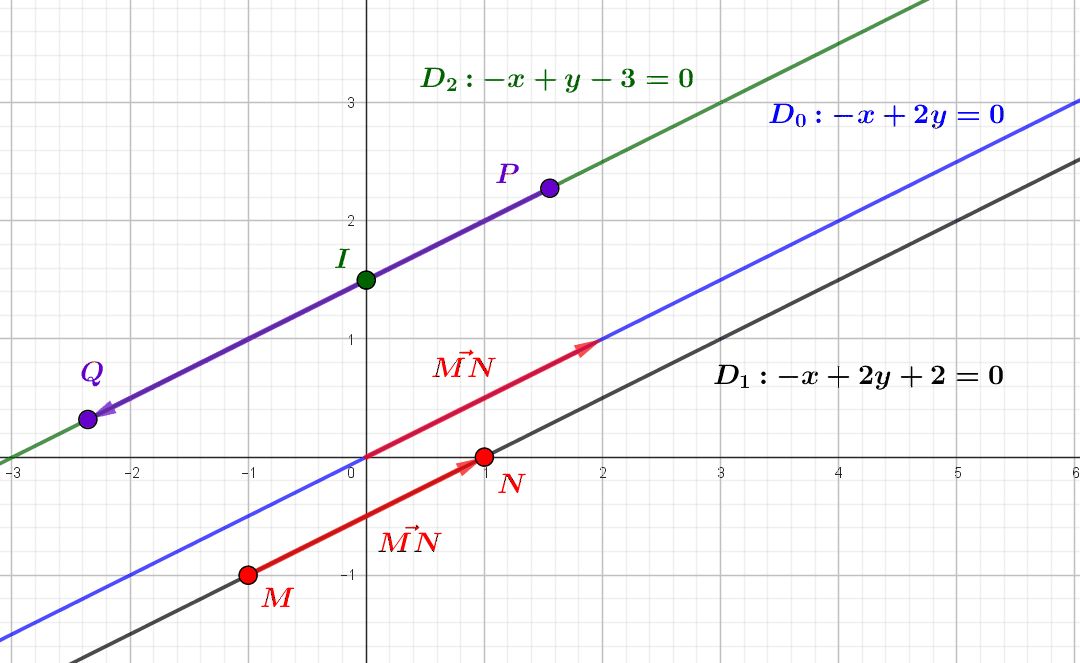
par Jean Barbet | Avr 21, 2023 | Algèbre, Géométrie
L’approche analytique de la géométrie plane, que nous devons à Descartes, permet de donner une description purement algébrique des droites du plan comme ensembles de solutions d’équations d’un seul type. Une telle équation, dite cartésienne, contient... 
par Jean Barbet | Mar 15, 2023 | Géométrie, Trigonométrie
Dans la géométrie intuitive on définit les aires des figures sans justification ou sans démonstration. Dans la géométrie euclidienne moderne, c’est-à-dire analytique, la définition de l’aire du triangle et du parallélogramme se fondent sur des définitions...





