par Jean Barbet | Juil 18, 2022 | Algèbre
Nous étudions la structure mathématique naturelle d’anneau, dont l’ensemble $\mathbb Z$ des entiers relatifs est le prototype, et qui permet d’interpréter de nombreux concepts de la théorie des nombres et de la géométrie, à travers notamment les... 
par Jean Barbet | Juin 28, 2022 | Algèbre, Nombres
La division des entiers naturels ne donne pas toujours un résultat entier, et la division euclidienne donne une meilleure approximation de ce résultat, sous la forme d’un quotient et d’un reste. On peut définir une addition et une multiplication...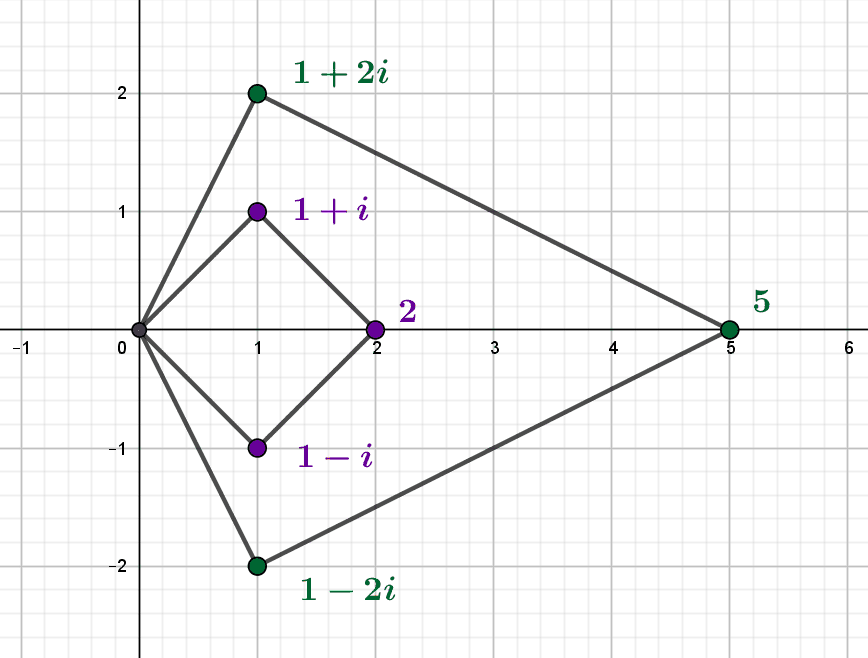 
par Jean Barbet | Mai 28, 2022 | Algèbre, Nombres
Nous savons que les nombres premiers ne demeurent premiers dans l’anneau \(\mathbb Z[i]\) des entiers de Gauss que lorsqu’ils sont sommes de deux carrés. En considérant leurs congruences modulo \(4\), il est possible d’en dire plus : on peut les... 
par Jean Barbet | Jan 14, 2022 | Nombres
En utilisant la somme des premiers nombres impairs dans l’ordre, on peut définir un algorithme simple de calcul de la racine carrée des nombres entiers avec une précision décimale arbitraire. 1.Calcul de la somme des \(n\) premiers entiers naturels impairs Il... 
par Jean Barbet | Déc 23, 2021 | Nombres
Dans cet article, nous abordons la question du « comptage » des nombres réels, autrement dit de la détermination du cardinal de l’ensemble \(\mathbb R\). Celui-ci est strictement supérieur au cardinal de l’ensemble des nombres rationnels, ce que nous...