
par Jean Barbet | Juin 18, 2024 | Analyse, Fonctions
Nous revenons dans cet article sur les fonctions monotones d’une variable réelle. Les propriétés de l’analyse des fonctions d’une variable réelle sont celles qui sont associées à la structure de la droite réelle. L’ordre entre nombres réels,... 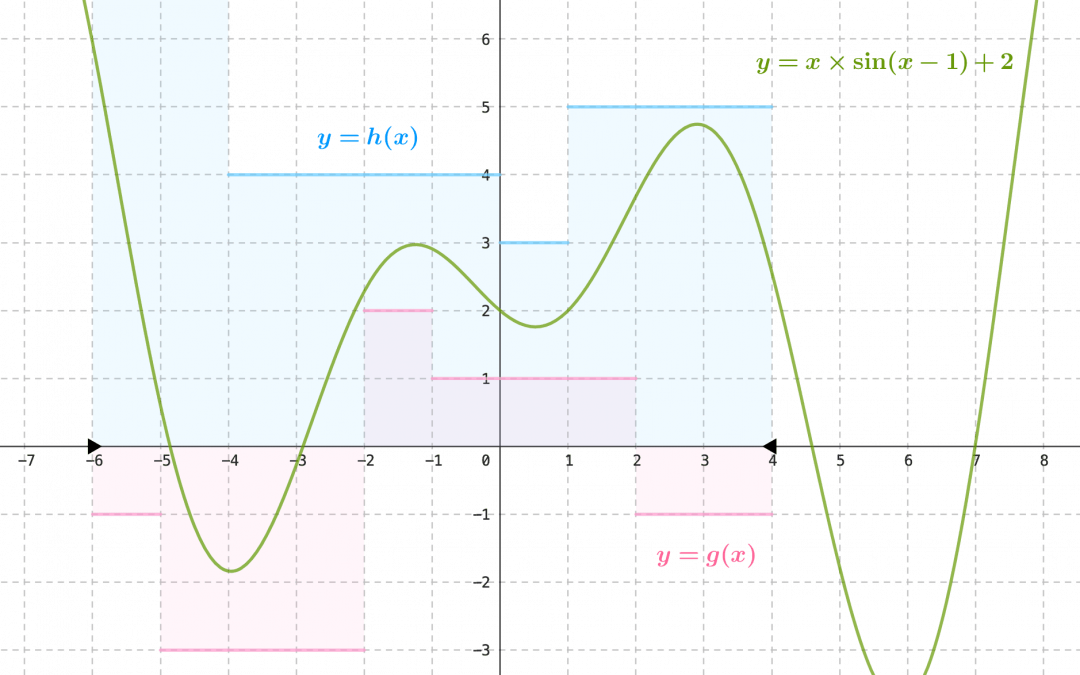
par Jean Barbet | Avr 11, 2024 | Analyse, Fonctions
Quelle est l’opération inverse de la dérivée d’une fonction ? Une première réponse à cette question consiste à intégrer une fonction qu’on veut pouvoir considérer comme dérivée, afin d’en construire une primitive. Cette problématique conduit... 
par Jean Barbet | Mar 7, 2024 | Algèbre, Ensembles, Fonctions, Nombres
Les fractions rationnelles à une indéterminée apparaissent à la convergence de la théorie des fonctions rationnelles et de la théorie des polynômes. En généralisant la construction des nombres rationnels à partir des nombres entiers relatifs, on les construit comme... 
par Jean Barbet | Fév 19, 2021 | Fonctions, Nombres
Introduction Lorsque nous avons introduit l’exponentielle circulaire, les fonctions trigonométriques cosinus et sinus ont été définies comme sa partie réelle et sa partie imaginaire. Nous en avons alors tiré les expressions analytiques : \(\cos... 
par Jean Barbet | Jan 8, 2021 | Analyse, Fonctions
A partir de la fonction exponentielle complexe, on peut définir une fonction « exponentielle circulaire », qui « enroule » la droite réelle sur le cercle trigonométrique, et permet de définir rigoureusement les fonctions trigonométriques cosinus et sinus, qui... 
par Jean Barbet | Déc 28, 2020 | Analyse, Fonctions
Certaines fonctions indéfiniment dérivables peuvent être décrites « autour de chaque point » comme la somme d’une série dite « entière ». Il s’agit des fonctions analytiques, réelles ou complexes, dont l’exemple typique est celui de la fonction...






