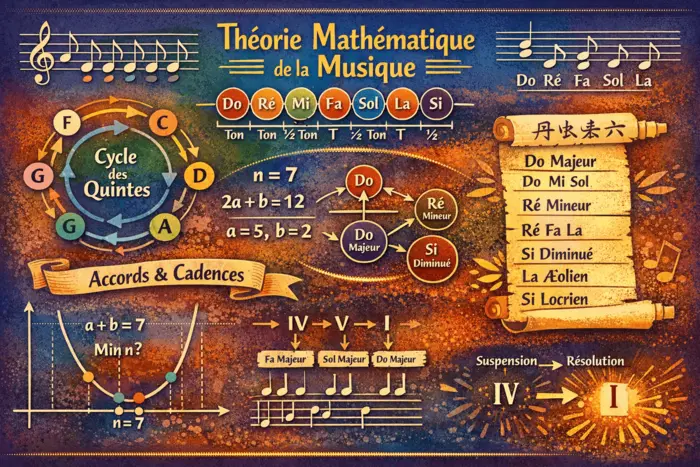
par Jean Barbet | Jan 22, 2026 | Musique, Nombres
Si la mélodie et l’harmonie sont les deux dimensions du tissu musical qu’est le contrepoint, l’harmonie désigne la superposition instantanée des différentes voix, dans une forme de résonance esthétique fondée sur la consonance. Elle s’intéresse... 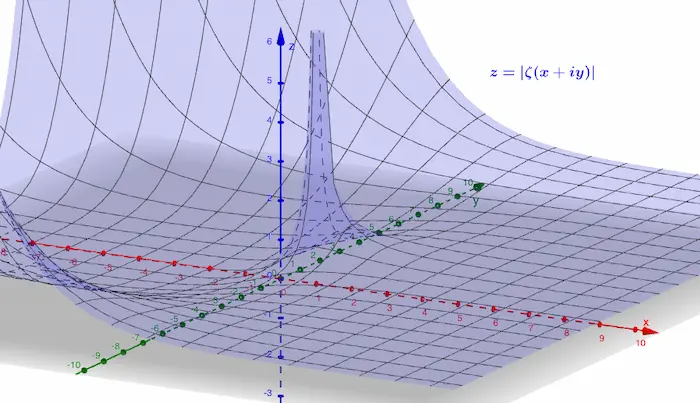
par Jean Barbet | Oct 23, 2025 | Analyse, Fonctions, Nombres
Les séries de nombres réels et complexes sont une manière alternative de considérer les suites de tels nombres comme sommes infinies de termes. Cette représentation des suites est particulièrement appropriée dans la théorie des nombres, où certains nombres sont... 
par Jean Barbet | Oct 1, 2025 | Musique, Nombres
On dit, peut-être d’après Platon, que la musique adoucit les mœurs. Vibration mélodique et harmonique, qui trouve son origine culturelle dans la prosodie du langage naturel et son fondement dans des rapports entiers de fréquences sonores, la musique envahit la... 
par Jean Barbet | Juil 22, 2025 | Logique, Ontologie
Quel est le fondement dernier de la mathématique comme science de l’infini ? Il ne peut s’agir de la logique mathématique, qui renvoie toujours elle-même à la question de l’être à travers les multiplicités que sont les ensembles. C’est donc... 
par Jean Barbet | Juin 27, 2025 | Algèbre, Fonctions, Géométrie
Les applications affines du plan euclidien sont celles qui préservent sa structure affine, c’est-à-dire essentiellement l’alignement des points et le parallélisme des droites. Ce critère permet d’en donner une définition analytique,...





