par Jean Barbet | Jan 22, 2026 | Musique, Nombres
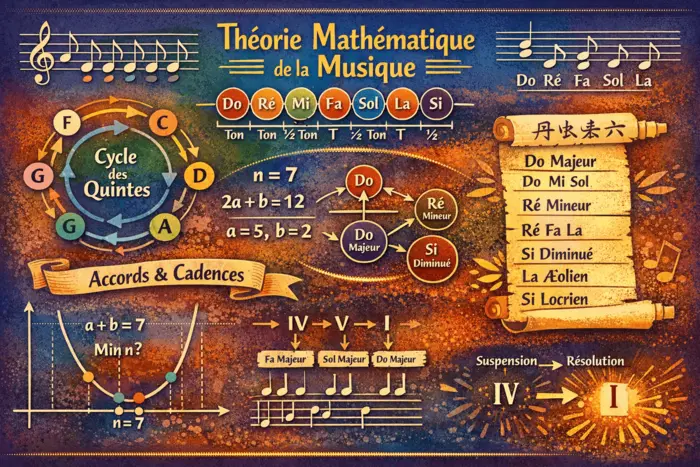
Si la mélodie et l’harmonie sont les deux dimensions du tissu musical qu’est le contrepoint, l’harmonie désigne la superposition instantanée des différentes voix, dans une forme de résonance esthétique fondée sur la consonance. Elle s’intéresse... 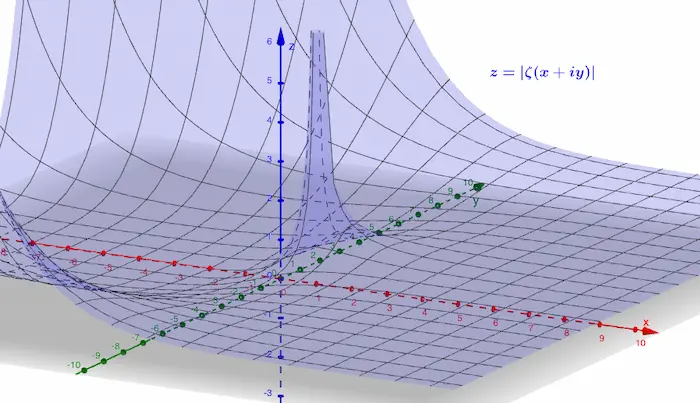
par Jean Barbet | Oct 23, 2025 | Analyse, Fonctions, Nombres
Les séries de nombres réels et complexes sont une manière alternative de considérer les suites de tels nombres comme sommes infinies de termes. Cette représentation des suites est particulièrement appropriée dans la théorie des nombres, où certains nombres sont... 
par Jean Barbet | Oct 1, 2025 | Musique, Nombres
On dit, peut-être d’après Platon, que la musique adoucit les mœurs. Vibration mélodique et harmonique, qui trouve son origine culturelle dans la prosodie du langage naturel et son fondement dans des rapports entiers de fréquences sonores, la musique envahit la... 
par Jean Barbet | Mar 11, 2025 | Analyse, Ensembles, Fonctions, Nombres
Les fonctions continues à valeurs réelles forment le concept fondamental de l’analyse réelle et de la topologie. Or, si la notion de continuité est transparente sur le plan de l’intuition, sa formulation mathématique nécessite une traduction, par exemple à... 
par Jean Barbet | Fév 6, 2025 | Algèbre, Géométrie, Nombres
L’algèbre linéaire transforme notre compréhension de l’espace grâce à une approche mathématique qui étend les concepts des espaces euclidiens à des structures plus abstraites comme les espaces vectoriels. Cet article explore comment des concepts simples... 
par Jean Barbet | Déc 2, 2024 | Ensembles, Logique, Nombres
Nous explorons la fondation de l’arithmétique naturelle en partant des axiomes de Peano au sein de la théorie des ensembles, révélant une approche innovante pour conceptualiser les nombres entiers naturels. Nous questionnons l’usage traditionnel des...






