The derivative of a function is its instantaneous variation, i.e. the slope of the tangent to the graphical representation of the function at that point.

1. General idea: an instantaneous variation

We place ourselves here in the framework of functions of a real variable, let us say functions \(f:I:\to\mathbb R\) defined on an open interval \(I\) of \(\mathbb R\) and with values in \(\mathbb R\). \(I\) is therefore a set of the form \(]a,b[=\{x\in \mathbb R : a<x<b\}\), for \(a<b\) real numbers or one of the symbols \(-\infty\) or \(+\infty\). To say that such a function \(f:I\to\mathbb R\) is derivable at a point \(t\in I\), is to say intuitively that this function \(f\) has an “instantaneous variation at the point \(t\)”. When this is the case, this instantaneous variation, being a real number noted \(f'(t)\), thus has a sign (positive or negative), which gives us the direction of the variation, and a magnitude (its absolute value \(|f'(t)|\)), which gives us the intensity of the variation.

2. Growth rate, monotonicity ratio and derivative

2.1. Monotonicity ration and geometric interpretation

To clarify the notion of derivative, we need to define the variation of the function \(f\) between two points. The point \(t\in I\) being given, if \(x\in I\) is another point the variation of \(f\) between \(t\) and \(x\) is the ratio of the variation between \(t\) and \(x\) and the variation between the values \(f(t)\) and \(f(x)\) of \(f\) at these two points. This growth rate of \(f\) between \(f(t)\) and \(f(x)\), mathematically called the monotonicity ratio, is therefore the ratio \(\frac{f(x)-f(t)}{x-t}\) (it is assumed that \(x\neq t\), in order to be able to divide by \(x-t\)). The monotonicity ratio has a simple geometric interpretation: it is the slope of the line joining the point of coordinates \(t,f(t))\) and the point of coordinates \(x,f(x))\), situated on the graph (graphic representation) of the function \(f\).

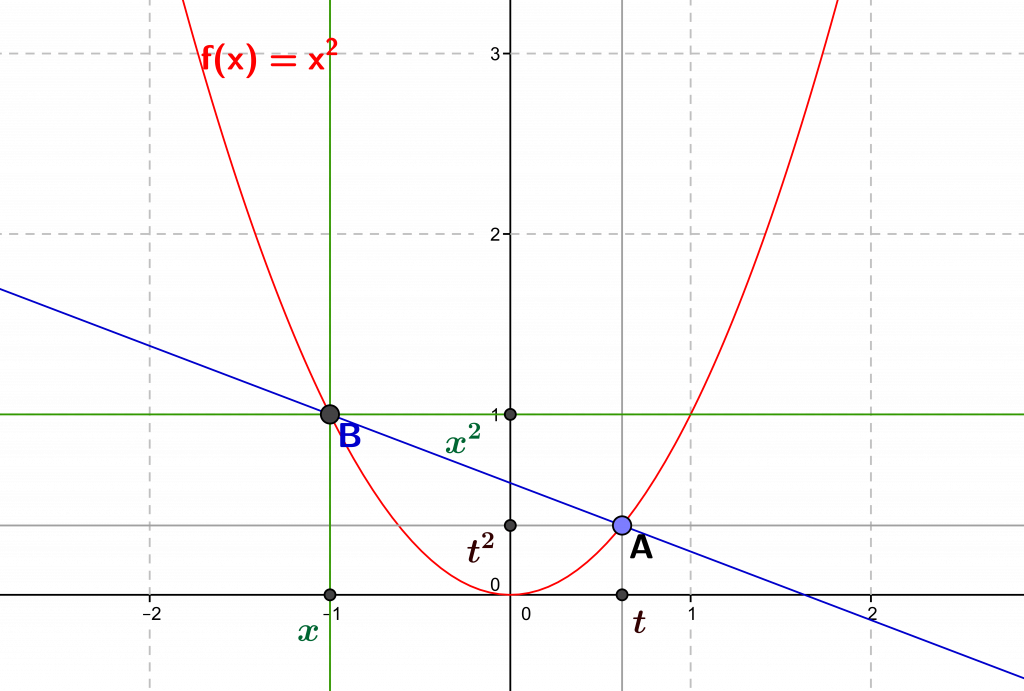
On the following figure, we have represented in red the graph of the square function \(f(x)=x^2\), and placed two points: \(A\), with coordinates \((t,t^2)\) (i.e. \((t,f(t))\) and \(B\) with coordinates \((x,x^2)\) (i.e. \((x,f(x))\).

2.2. Instantaneous variation and derivative at a point

If we assimilate the abscissae (i.e. the values of the variable) to “time”, the variation represented by the monotonicity ratio takes place “over a certain time”. The notion of the derivative of \(f\) as an “instantaneous” variation then considers this time as “infinitely small”: this corresponds to the values of the monotonicity ratio, i.e. the slope of the line joining the points \(t,f(t))\) and \(x,f(x))\), “as \(x\) approaches the fixed point \(t\) indefinitely”. Mathematically, this is interpreted as the search for the limit of the ratio \(\frac{f(x)-f(t)}{x-t}\) “when \(x\) tends towards \(t\)” (\(t\) being fixed, and \(x\neq t)\). Thus, the function is said to be derivable at \(t\) if the limit \(\lim\limits_{x\to t}\frac{f(x)-f(t)}{x-t}\) exists, and this limit is then by definition the derivative of the function \(f\) at \(t\).

Geometrically, we can then consider the derivative \(f'(t)\) as the limit of the slope of the line joining \((t,f(t))\) and \((x,f(x))\) when \(x\) approaches \(t\), in other words as the slope of the line obtained for \(x=t\), that is to say the slope of the tangent line to the graph of \(f\) at the point \((t,f(t))\). On the following figure, we have taken the graphical representation of the function \(f(x)=x^2\) and of the straight line joining the fixed point \(A\) of coordinates \(t,f(t))\) and the mobile point \(B\) of coordinates \((x,f(x))\), which we move according to the values of \(x\).

On the same figure as before, imagine that the abscissa \(x\) of the point \(B\) approaches the abscissa \(t\) of the point \(A\) : the line approaches the tangent line at the point \(A\), whether \(x<t\) or \(x>t\). The search for the limit of the monotonicity ratio indeed includes the two cases where \(x>t\) (when \(x\) is to the “right” of \(t\)) and where \(x<t\) (when the point \(x\) is to the “left” of \(t\)).

2.3. To sum up: derivative of a function at a point

– when \(f\) is derivable at \(t\in I\), the monotonicity ratio \(\frac{f(x)-f(t)}{x-t}\) approaches a growth rate \(f'(t)\) corresponding to values of \(x\) closer and closer to \(t\)
– geometrically, the slope of the line joining the points \((t,f(t))\) and \((x,f(x))\) approaches the slope of the tangent to the graph of the function \(f\) at the point \((t,f(t))\), which is the derivative \(f'(t)\)
– The derivative \(f'(t)\) of \(f\) at the point \(t\) is thus the “instantaneous variation” of the function \(f\), analogous to the “velocity” of a trajectory.

3. Derivative function

3.1. Derivative function of a derivable function

Having said this, we have described the derivative \(f'(t)\) of a function (\(f:I:\to\mathbb R\)) at a point (\(t\in I\)). One should not confuse \(f'(t)\), which is a number for which we have given a geometric interpretation, with the derivative function \(f’\) of a function \(f\). Just as a function does not always have a derivative at every point of its domain, a function does not always have a derivative function. The function \(f:I\to\mathbb R\) is said to be derivable if \(f\) is derivable at any point \(t\) of \(I\), in other words if the function \(f\) has a derivative \(f'(t)\) at any point \(t\) of \(I\). In this case, we then call the derivative of \(f\) the function noted \(f’\), defined on the same interval \(I\), and which value at \(t\in I\) is the real number \(f'(t)\). This explains the notation introduced earlier for this number.

3.2. Geometric interpretation of a derivative function

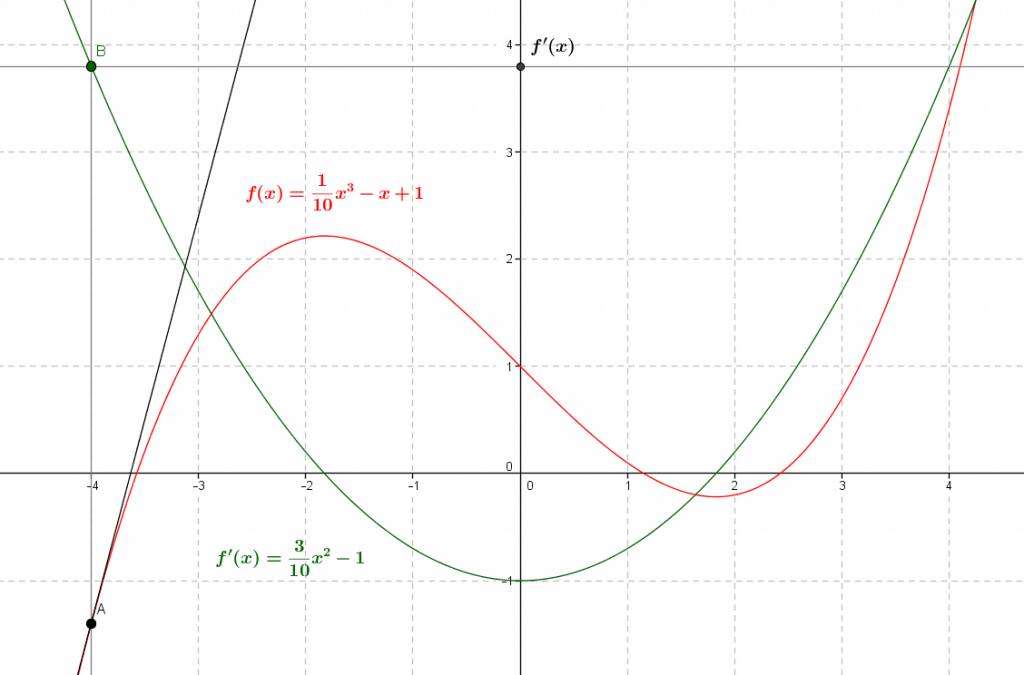
We can give a geometric interpretation of the derivative function, returning to that of the derivative at a point: the graph of the derivative function thus represents the slope of the tangent to the initial function at each point. In the following figure, we have plotted in red part of the graph of the function \(f(x)=(1/10)x^3-x+1\), derivable on the whole interval \(I=\mathbb R\), and in green its derivative function \(f'(x)=(3/10)x^2-1\). The tangent at the point \(A\) of coordinates \((x,f(x))\) is represented in black.

4. Primary use of the derivative

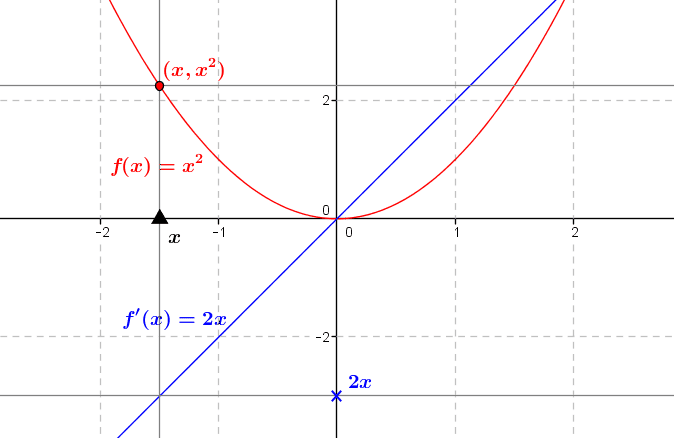
The primary and fundamental use of the derivative is the study of the variations of a function. When the numerical function \(f:I\to\mathbb R\) is derivable on \(I\), the study of the derivative function \(f’:I\to\mathbb R\) indeed makes it possible to know how \(f\) varies on all the interval \(I\). We study the sign of the function \(f’\) on \(I\), which makes it possible for example to identify the parts of \(I\) where \(f\) is increasing (where the derivative is positive), or decreasing (where the derivative is negative). Using the example of the square function \(f:\mathbb R\to\mathbb R\), \(x\mapsto x^2\), the function \(f'(x)\) is given by the expression \(2x\): on the interval \(]-\infty,0]\) one has \(f'(x)\leq 0\) so \(f\) is decreasing, on the interval \([0,+\infty[\) one has \(f'(x)\geq 0\) so \(f\) is increasing.

On the following figure, we represented the function \(f(x)=x^2\) and its derivative \(f'(x)=2x\): one checks that \(f'(x)\leq 0\) for \(x\leq 0\) (where the function \(f\) is decreasing) and that \(f'(x)\geq 0\) for \(x\geq 0\) (where the function \(f’\) is increasing).