The definition of a circle is simple: it is a set of points located at the same distance from a given point. This distance is called the radius and this point is called the centre of the circle.

1. Circles as sets of solutions of an equation

But what is a point, and what is a distance? If we have a very clear intuition, this one is not sufficient to speak in a rigorous way about these things in mathematics.

We mentioned in the article The Euclidean Plane: Ancient Geometry and the Analytical Approach how it is possible to give a precise meaning to the notion of a point and the notion of a distance in the framework of the modern Euclidean plane. Thanks to the modern construction of real numbers, every positive real number has a square root, and two points \(M\) and \(N\) being represented by their respective coordinates \((x,y)\) and \((t,u)\) in the Cartesian approach to geometry, the distance \(d(M,N)\) between these two points is the square root of the sum of the squares of the distances between their coordinates, i.e. \(d(M,N)=\sqrt{(x-t)^2+(y-u)^2}\), which is a reformulation of the Pythagorean theorem.

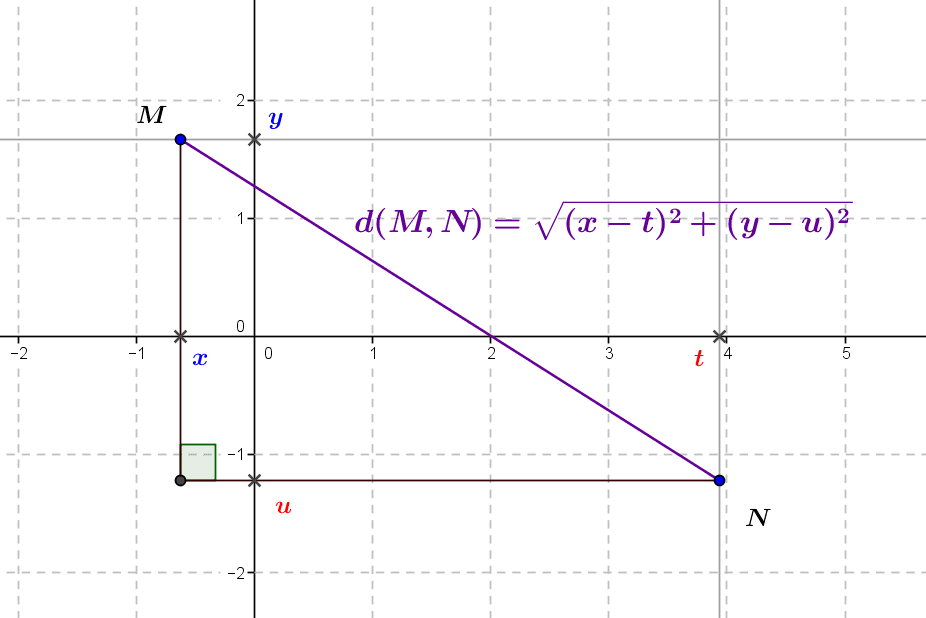
From this point of view, we have a perfectly clear “analytical” description of what a circle is in the plane, from the definition at the start: the circle \(C\) with centre \(I=(a,b)\) and radius \(R\) (positive real number) is the set of points \(M=(x, y)\) of the plane \(\mathbb R^2\) such that the distance \(d(I,M)\) between \(I\) and \(M\) is \(R\), that is, since the distance \(d(I,M)\) is \(\sqrt{(x-a)^2+(y-b)^2} \), symbolically \[\mathscr C=\{(x,y)\in\mathbb R^2 | \sqrt{(x-a)^2+(y-b)}=R\}.\] As the number \(R\) is positive, we can then do without the square root to finally describe the circle \(C\) as the set \[\mathscr C=\{(x,y)\in \mathbb R^2 | (x-a)^2+(y-b)^2=R^2\},\] \which gives us the typical equation of a circle in the plane, here \((x-a)^2+(y-b)^2=R^2\) for the circle \(C\) with centre \(I=(a,b)\) and radius \(R\).

In other words, such a circle is the set of solutions \((x,y)\) of this equation: thanks to Descartes’ analytical method, we can describe a circle in the plane as a set of solutions of an equation, in a way analogous to the description of a line as a set of solutions of an equation. For example, the circle at the beginning has equation \((x+1)^2+(y+\frac 3 2)^2=6\).

2. The trigonometric circle : Cosine and Sine as angular coordinates

Now, we have at our disposal by means of real analysis (the theory of functions of the set \(\mathbb R\)) two functions, cosine and sine, known as “trigonometric”, and which give us the coordinates of a point of the trigonometric circle, which is the circle with centre \(O=(0,0)\) and radius \(1\). Indeed, a point \(M=(x,y)\) on this circle is marked by the angle it describes with the axis \([0x)\), which is measured as the (oriented) length of the circular arc bounded by the point \(I=(0,1)\) and the point \(M\), which is called the measure in radians of the angle \(\widehat{IOM}\). In other words, if the length of the arc \(\overset{\frown}{IM}\) is \(t\), the (Cartesian) coordinates of the point \(M\) are \(x=\cos t\) and \(y=\sin t\) : the cosine and sine of the angle \(t\) are the projections of the point \(M\) on each axis.

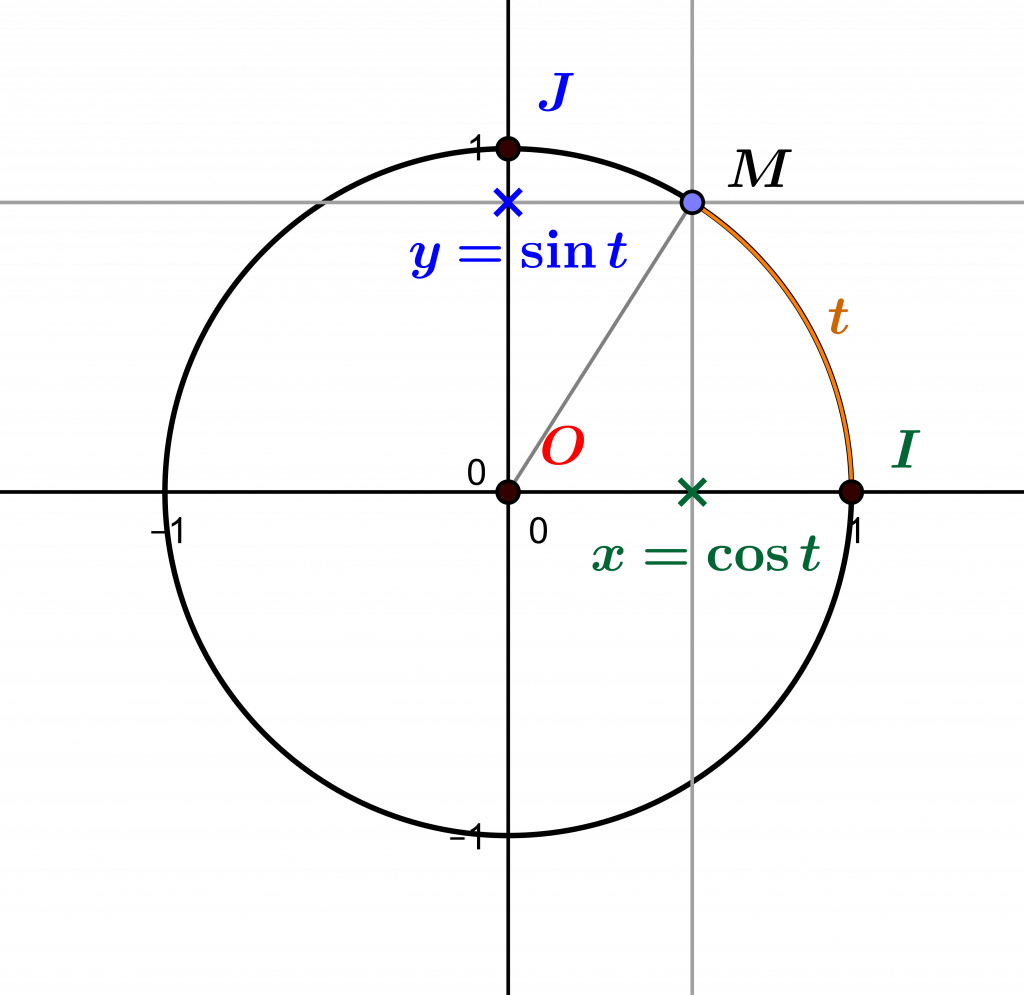
Since the radius of the trigonometric circle is equal to \(1\), this means by the Pythagorean theorem that, the angle determined by the point \(M\) being equal to \(t\), we have the equality \(cos^2 t+sin^2t=1\). In general, for any real number \(t\) this equality is true and \(\cos t\) and \(\sin t\) are the coordinates of a point of the trigonometric circle: in other words, the couples of real numbers \((x,y)\) of the form \(x=cos t\) and \(y=sin t\) verify the equation \(x^2+y^2=1\), which is the equation of the trigonometric circle, since it can be rewritten as \((x-0)^2+(y-0)^2=1^2\), which, as we have seen, is the equation of the circle with centre \((0,0)\) and radius \(1\). Conversely, any point \((x,y)\) verifying this equation, is on the trigonometric circle, and is of the form \(\cos t,\sin t\) as we have discussed, for a real number \(t\) taken in the interval \([0,2\pi[=\{x(t)\in \mathbb R | 0\leq t<2\pi\}\).

3. Parameterising a circle: going from an equation to a plot

We can therefore adopt another approach to describe the trigonometric circle, i.e. describe it by a parameter, which is mathematically equivalent to “plotting” it in the plane, using a function \(f:[0,2\pi[\to \mathbb R^2\) : a function is a mathematical operation that “transforms” one object into another; here, the transformed object is the parameter \(t\) (a real number greater or equal to \(0\) and lesser than \(2\pi\)), and the result of the transformation is the point \(f(t)=(\cos t,\sin t)\) of the plane, which describes the “value of the function \(f\) at point \(t\)”. When \(t\) takes all the values between \(0\) and \(2\pi\), then \(f(t)\) takes as values all the points of the trigonometric circle; if we represent \(t\) as “time”, we have conceptualised the drawing of the trigonometric circle, in contrast with its definition by an equation. We say that we have parameterised this circle, that the function \(f\) is a parametrisation of the trigonometric circle.

Using this parametrisation, we can then describe a parametrisation, a “plot”, of any circle in the plane – at least if its radius is not zero – by returning to the description by an equation. If, as before, \(\mathscr C\) is the circle with centre \(I=(a,b)\) and radius \(R>0\), whose equation is \((x-a)^2+(y-b)^2=R^2\), a point \(M=(x,y)\) is on \(\mathscr C\) if and only if the preceding equation is verified. Now, this equation can be rewritten in the following form: dividing by \(R^2\) on each side, it is equivalent to the equation \[\left(\dfrac{x-a}{R}\right)^2+\left(\dfrac{y-b}{R}\right)^2=1,\] so that the point \(M=(x,y)\) is on the circle \(\mathscr C\) if and only if the point \((\frac{x-a}{R},\frac{y-b}{R})\) is on the trigonometric circle! This is equivalent to having \(x=a+R\cos t\) and \(y=a+R\sin t\), so we can “draw” the circle \(\mathscr C\) thanks to the parametrisation \(g:[0,2\pi[\to \mathbb R^2\) defined by \[g(t)=(a+R\cos t,a+R\sin t).\] One could replace the interval \([0,2\pi[\) by another interval, or change the “speed” of the plot, but the main point here is to remember that a circle in the plane can be defined either by an equation or by a parameter, and that one can switch from one description to the other. These are the two fundamental ways of describing a geometric object.