The trigonometric circle allows us to define the cosine, sine and tangent of an oriented angle, and to give an interpretation through Thales’ and Pythagoras’ theorems.

Introduction: trigonometry and functions

Trigonometry is the study of the relationships between angles and the lengths of the sides in a triangle, and by extension of trigonometric functions such as sine, cosine and tangent.

In this article, we propose a definition of the sine, cosine and tangent of an oriented angle from the trigonometric circle, and a geometric interpretation naturally associated with Thales and Pythagoras theorems.

1. The trigonometric circle and the circular representation of angles

1.1. Practical units and oriented angles

The practical measuring units of angles are the degree and the grade; a full angle (i.e. a complete turn) measures 360 degrees or 400 grades, a flat angle (i.e. a half turn) measures 180 degrees or 200 grades, a right angle (i.e. a quarter turn) measures 90 degrees or 100 grades.

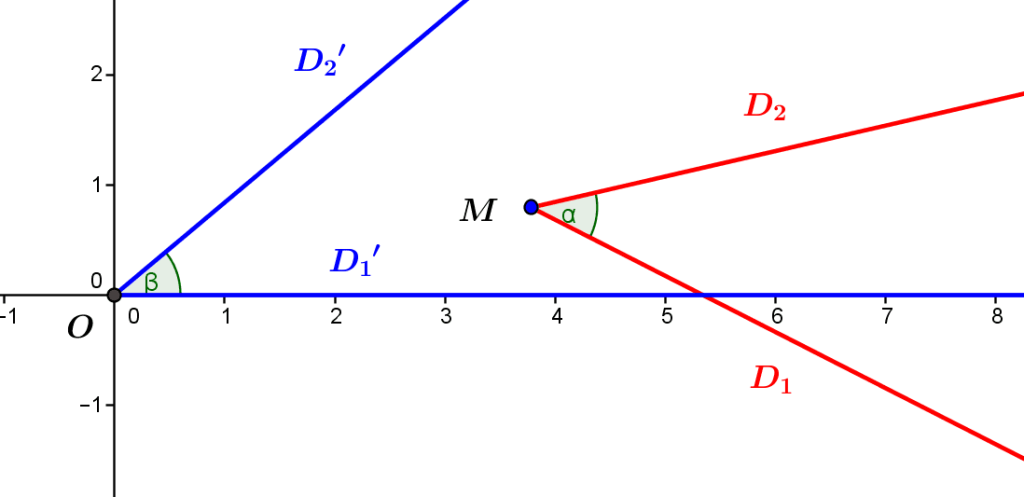
We will speak here of oriented angles. Such an angle is represented by two half-lines based at the same point, and its measurement is considered positive in the direct direction (i.e. rotational or counter-clockwise). Carrying out a translation and a rotation, we can always represent such an angle from the origin of the plane, taking as the first half-line the half-axis of the positive abscissas (see the following figure).

In order to speak about the measure of an oriented angle, it is necessary to give it a sign. For example, a half turn to the left corresponds to an angle of 90 degrees while a half turn to the right corresponds to an angle of -90 degrees.

1.2. The measurement of angles in radians

The mathematical, i.e. theoretical, measure unit of oriented angles is the radian. A full angle measures \(2\pi\) radians, a flat angle \(\pi\) radians, and a right angle \(\pi/2\) radians. What does this way of measuring angles correspond to, in other words what does this measuring unit correspond to?

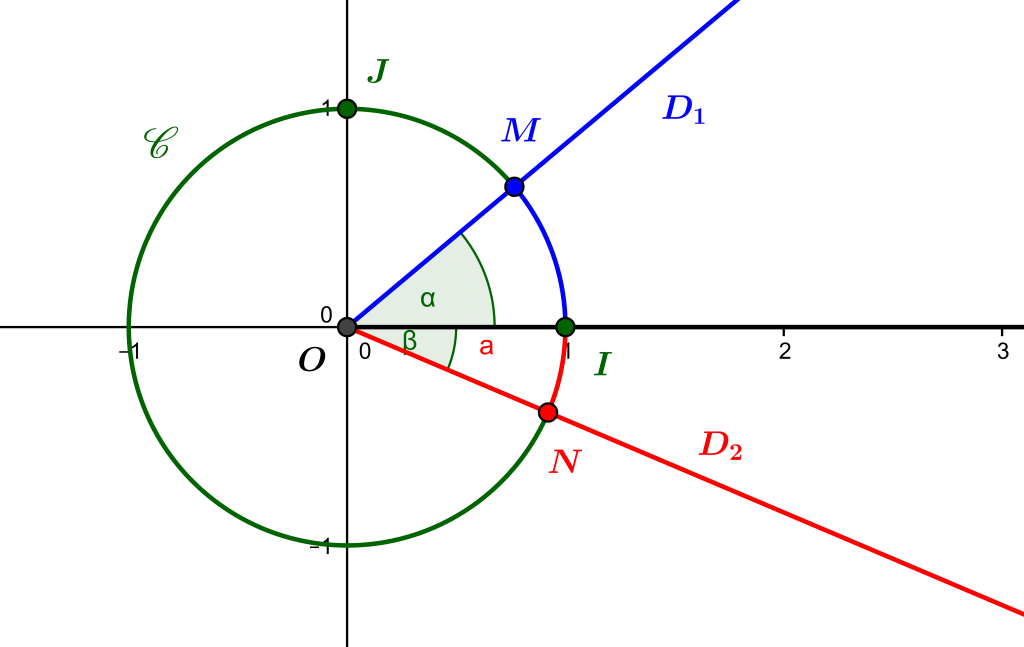
The measurement of angles in radians, positive or negative if we are talking about oriented angles, is relative to the representation of angles on the circle with centre ((0,0)\) and radius \(1\) (see Drawing a circle on the plane: equations and parameters), which is called the trigonometric circle.

An angle oriented between two half-lines being related to the origin of the Euclidean plane and to the half-axis of the positive abscissae, the first half-line identified with the positive part of the angle of the abscissae, one considers the intersection of the second half-line with the trigonometric circle.

This intersection is a point in the plane, which determines the end of an arc of circle based on the point \((1,0)\) (noted \(I\)). By definition, the measure of the angle, in radians, is the length of this arc of circle, with a sign according to the orientation of the angle (i.e. whether the arc is run in the direct or indirect sense).

Thus, the measure of the perimeter of the trigonometric circle is the measure of the direct full angle; that of the direct flat angle is \(\pi\) and the measure of the direct right angle is \(\pi/2\).

2. The trigonometric functions of angles

2.1. The circular coordinates

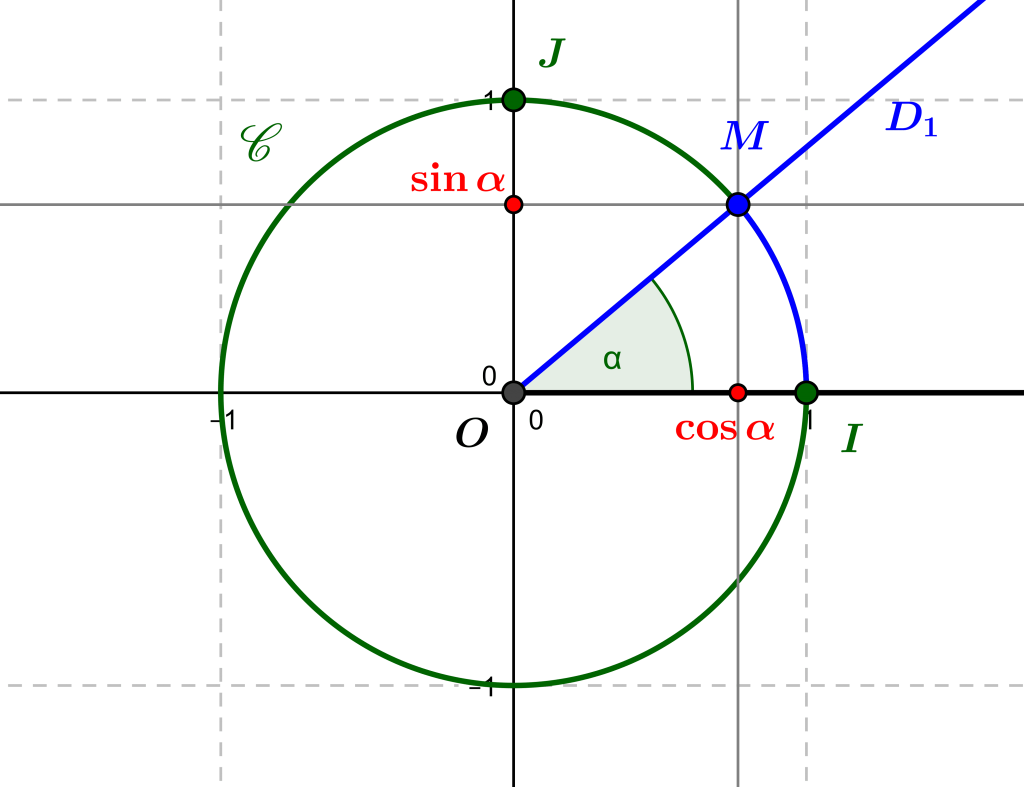
Thus, an oriented angle can always be represented by a point of the trigonometric circle.

Now, by considering the coordinates of this point (see The Euclidean Plane: Ancient Geometry and the Analytical Approach), that is to say by projecting this point on the x-axis on the one hand, and on the y-axis on the other hand, we obtain two real numbers, which are the coordinates of the point, and which we will call the circular coordinates of the initial angle.

The first circular coordinate of the angle, obtained as the abscissa of the point it determines on the trigonometric circle, is called the cosine of the angle. We note \(\ cos\alpha\) the cosine of an oriented angle. \(\alpha\).

The second circular coordinate of the angle, obtained as the ordinate of the point it determines on the trigonometric circle, is called the sine of the angle. We note \(\sin\alpha\) the sine of an oriented angle \(\alpha\).

It should be noted that the cosine and the sine are defined here for an oriented angle and not for a real number! It is thus a question of the circular co-ordinates of a geometrical quantity, and not of the cosine and the sine of a real number, which are fundamentally associated with the cosine and the sine of an angle, but are associated with numerical quantities.

2.2. Trigonometric functions

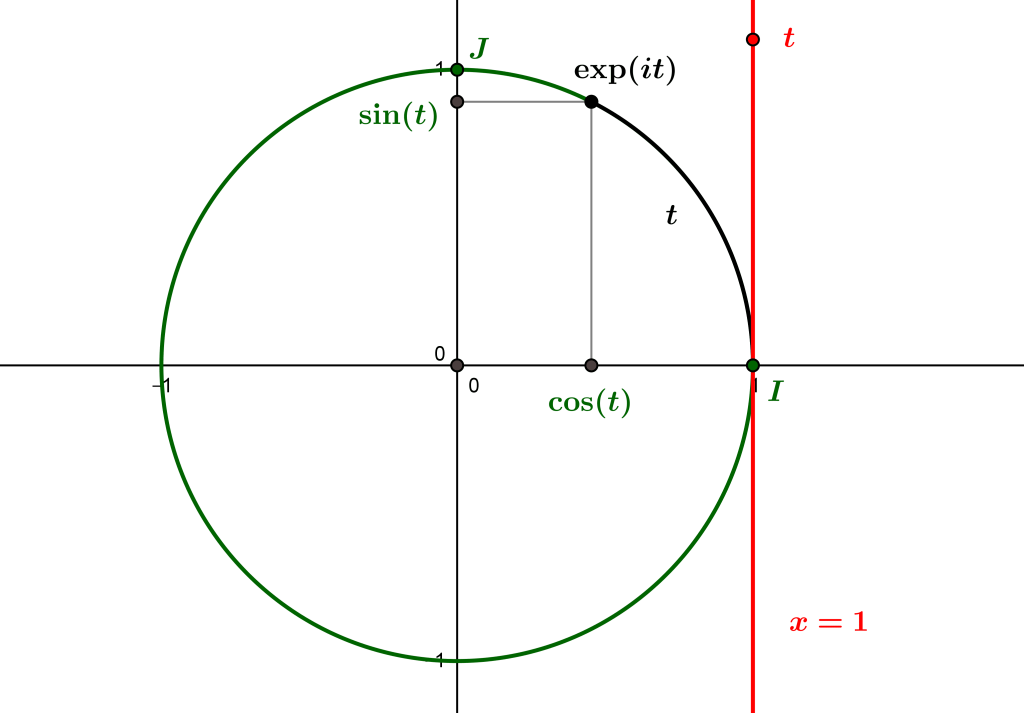
The cosine and sine of an angle (a geometric object) should not be confused with the cosine and sine of a real number, namely the functions of a real variable, defined for any real number \(x\), and noted (\cos\) and [\sin\). There exists however a fundamental relationship between the two, which can be explained as follows. If we consider the vertical line tangent to the trigonometric circle at point \(I\), i.e. the line with equation \(x=1\), then we can imagine “wrapping” this line around the trigonometric circle, in the trigonometric (counter-clockwise) direction. In other words, the points of the line situated in the upper half-plane are mapped onto the trigonometric circle, starting at point \(I\), and carrying over to the circle the length corresponding to the ordinate of the point in the anti-clockwise direction.

This transformation is described rigorously from what can be called the circular exponential function, which associates to a real number \(t\), representing the ordinate of a point on the tangent line, the complex number \(\exp(it)\), representing the corresponding point of the trigonometric circle. This function appears in the trigonometric notation for complex numbers. To return to cosine and sine, a real number \(t\) being represented as the ordinate of a point of the vertical line, the point of the circle which is associated with it by this “winding” determines an oriented angle, of which one can consider the cosine and the sine. The cosine and the sine of the real number \(t\) are then those of the angle determined by the point of the circle associated with \(t\). This is why, in the trigonometric notation of the complex numbers, we write \(e^{it}=cos(t)+i\sin(t)\): the real numbers \(\cos (t)\) and \(\sin(t)\) are, respectively, the real and imaginary parts of the complex number \(e^{it}\), which is none other than \(exp(it)\).

3. Geometric interpretation: Thales and Pythagoras

3.1. The tangent and Thales’ theorem

There is another usual trigonometric function called tangent, and which is defined, for a real number \(x\) with non-zero cosine, as the quotient \(\dfrac{\sin x}{\cos x}\).

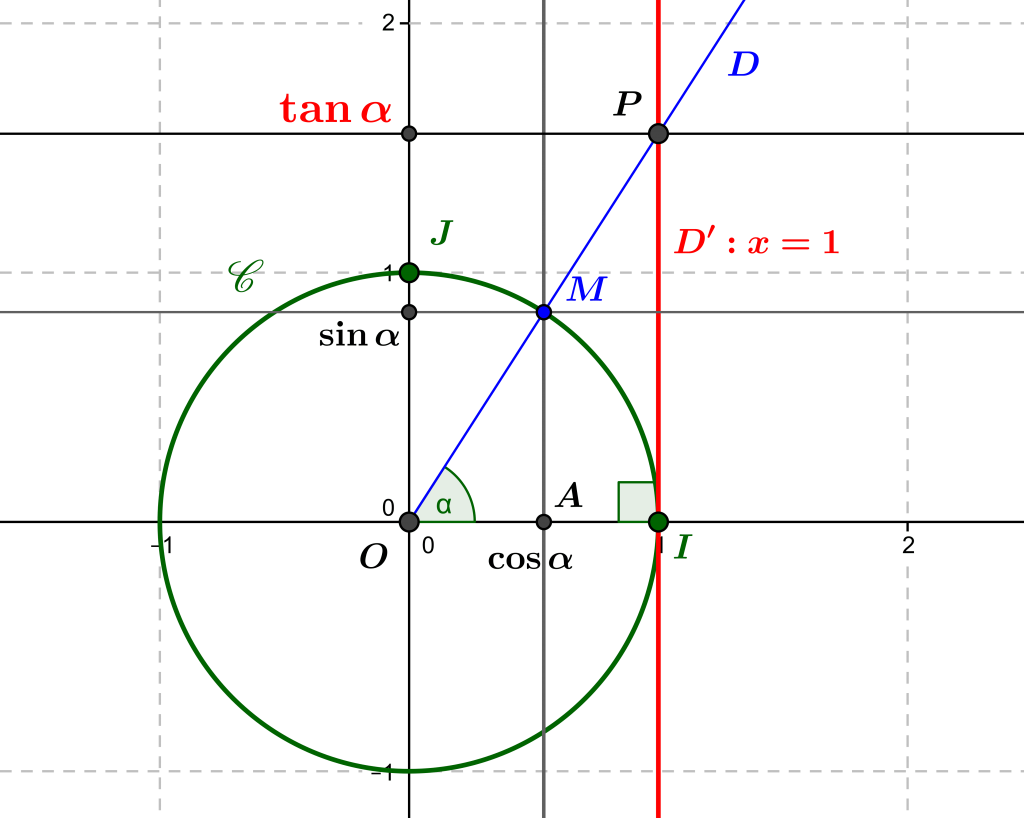
If we return to oriented angles, the tangent of such an angle can be defined geometrically as the ordinate of the intersection point \(P\) of the second half-line of the angle with the vertical line of equation \(x=1\), i.e. the tangent to the trigonometric circle.

To be able to define the tangent of an oriented angle in this way, it is therefore necessary for this angle to have a measure other than \(\pi/2\) or \(-\pi/2\), the case where the second half-line of the angle is vertical and therefore does not intersect with the line \(x=1\). This case corresponds, in terms of functions, to the situations where we cannot divide \(\sin x\) by \(\cos x\), because \(\cos x=0\).

If we denote by \(\alpha\) an oriented angle of measure different from \(\pi/2\) or \(-\pi/2\), we then denote by \(\tan\alpha\) the tangent of \(\alpha\). We adopt the same notation for the numerical function, i.e. \(\tan x=\dfrac{\sin x}{\cos x}\) for \(x\) a real number such that \(\cos x\neq 0\).

A natural geometric interpretation of the tangent of an oriented angle can be given, using Thales’ Theorem in the following way. Keeping the same notations as before, let us designate by \(P\) the intersection point of the second half-line (\(D)\) of the angle \(\alpha\) with the line \(D’\) of equation \(x=1\) (passing through \(I)\) and perpendicular to the x-axis). Let us also designate by \(A\) the point \((\cos\alpha, 0)\) which represents \(\cos\alpha\) on the x-axis.

The lines \(D’=(IP)\) and \((AM)\) are parallel, and in the triangle \(OIP\) rectangular at \(I\), by Thales’s theorem one can write the equality \(\dfrac{AM}{OA}=\dfrac{IP}{OI}\), that is to say \(\dfrac{\sin\alpha}{\cos\alpha}=\tan\alpha\).

3.2. Coordinates and the Pythagorean theorem

Returning to circular coordinates, we can interpret the other great elementary theorem of Euclidean plane geometry as a fundamental relationship between the sine and cosine.

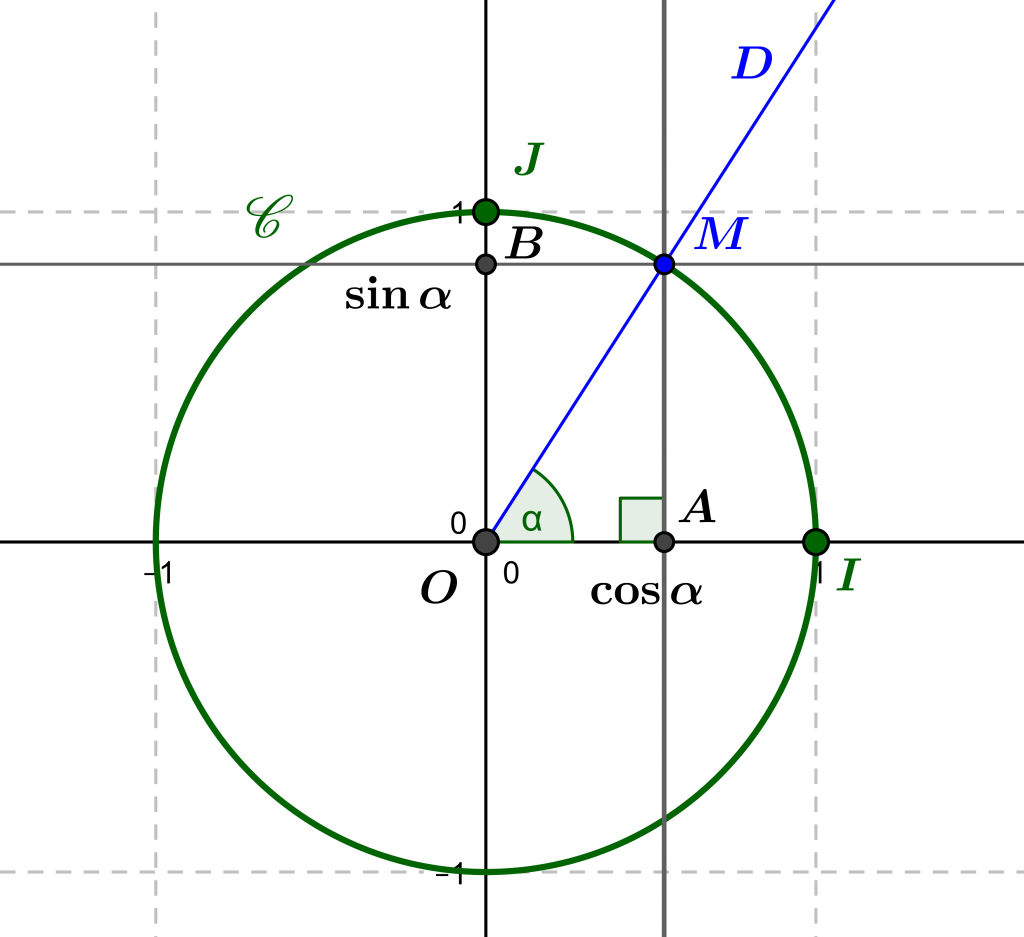
With the same notations, we consider from now on the triangle \(OAM\), rectangle in \(A\) and we note \(B\) the point \((0,\sin\alpha)\), which represents \(\sin\alpha\) on the ordinate axis.

By definition of \(A\) and \(B\), we have \(OA=\cos\alpha\) and \(AM=OB=\sin\alpha\), so that by the Pythagorean theorem, we have \(OA^2+OB^2=OA^2+AM^2=OM^2\), that is, \[\cos^2\alpha+sin^2\alpha=1,\], since \(OM=1\), the segment \([OM]\) being by definition a radius of the trigonometric circle.

This is the fundamental relationship between the sine and cosine of an oriented angle, which can be extended to the sine and cosine of a real number: for any real number \(x\), we have \(\cos^2x+\sin^2x=1\).

This relation allows, among other things, to parameterise the trigonometric circle and all the circles of the plane using the sine and cosine functions (see Drawing a circle on the plane: equations and parameters).