
par Jean Barbet | Mar 7, 2024 | Algèbre, Ensembles, Fonctions, Nombres
Les fractions rationnelles à une indéterminée apparaissent à la convergence de la théorie des fonctions rationnelles et de la théorie des polynômes. En généralisant la construction des nombres rationnels à partir des nombres entiers relatifs, on les construit comme... 
par Jean Barbet | Fév 9, 2024 | Algèbre, Géométrie
Le produit vectoriel représente une opération antilinéaire essentielle dans l’espace euclidien, transformant deux vecteurs en un troisième. Lorsque les deux vecteurs initiaux sont linéairement indépendants, ils forment, avec leur produit vectoriel — dont la... 
par Jean Barbet | Jan 19, 2024 | Algèbre, Géométrie, Nombres
Le plan euclidien acquiert une orientation naturelle par le choix d’une base, que l’on peut qualifier de directe ou d’indirecte. Cette orientation se manifeste à travers le signe du déterminant de la base, correspondant à l’aire algébrique du... 
par Jean Barbet | Nov 29, 2023 | Algèbre, Géométrie, Trigonométrie
Le produit scalaire et le déterminant sont des concepts clés de l’algèbre linéaire dans le plan euclidien, offrant une compréhension profonde des relations entre deux vecteurs $u$ et $v$. Lorsque ces vecteurs sont unitaires, leur produit scalaire et déterminant... 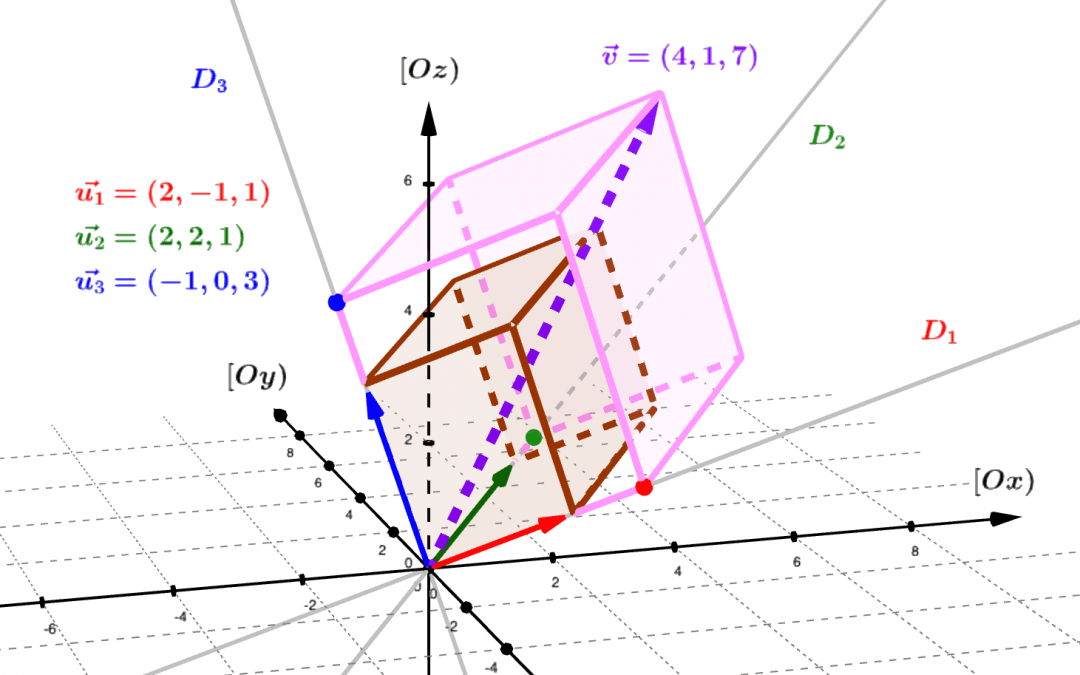
par Jean Barbet | Juil 3, 2023 | Algèbre, Géométrie
Comme dans le plan euclidien $\mathbb R^2$ , il existe dans l’espace euclidien $\mathbb R^3$ une infinité de bases ou « systèmes de représentation » des vecteurs : l’espace étant intuitivement de dimension 3, ces bases sont toujours formées de 3 vecteurs... 
par Jean Barbet | Juin 6, 2023 | Algèbre, Nombres
Les corps finis traduisent sur le plan structurel certaines propriétés arithmétiques et servent de « corps de restes » en théorie des nombres. Par analogie avec les corps $\mathbb R$ des nombres réels et $\mathbb C$ des nombres complexes, le nombre $-1$ peut y...






