la Règle et le Compas
Espace Mathématique
Une approche conceptuelle
de la science mathématique
Articles Récents
Anneaux d’entiers quadratiques et ramification des nombres premiers
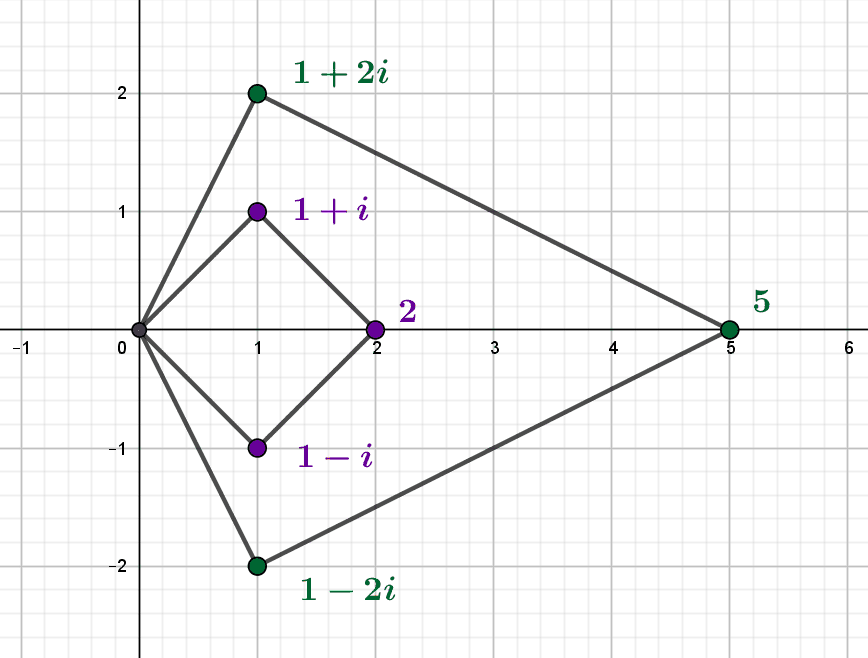
L'anneau des entiers de Gauss \(\mathbb Z[i]\) possède des propriétés remarquables, analogues à celles de l'ensemble \(\mathbb Z\) des nombres entiers relatifs. Il existe toute une famille de tels anneaux, possédant des propriétés similaires, et définis aussi à partir...
Les corps finis : une approche structurelle de l’arithmétique
Les corps sont les anneaux dont tout élément non nul est inversible. Tous les anneaux intègres finis sont des corps, et tous ces corps finis sont commutatifs. Avec un peu d'algèbre commutative, on peut même décrire entièrement tous les corps finis, qui correspondent...
Nombres premiers entre eux et inversion modulaire
Deux nombres entiers sont dits premiers entre eux si ils n'ont pas de facteur premier en commun : il sont donc premiers "l'un par rapport à l'autre". Le nombre des restes modulo un entier naturel non nul $n$ qui sont premiers avec $n$ est ce qu'on appelle l'indicateur...
Anneaux, homomorphismes et quotients
Nous étudions la structure mathématique naturelle d'anneau, dont l'ensemble $\mathbb Z$ des entiers relatifs est le prototype, et qui permet d'interpréter de nombreux concepts de la théorie des nombres et de la géométrie, à travers notamment les notions...
Division euclidienne et arithmétique modulaire
La division des entiers naturels ne donne pas toujours un résultat entier, et la division euclidienne donne une meilleure approximation de ce résultat, sous la forme d'un quotient et d'un reste. On peut définir une addition et une multiplication "modulaires" sur les...
Les nombres premiers imaginaires : ramification dans les entiers de Gauss
Nous savons que les nombres premiers ne demeurent premiers dans l'anneau \(\mathbb Z[i]\) des entiers de Gauss que lorsqu'ils sont sommes de deux carrés. En considérant leurs congruences modulo \(4\), il est possible d'en dire plus : on peut les classer en trois types...
Un algorithme de calcul de la racine carrée
En utilisant la somme des premiers nombres impairs dans l'ordre, on peut définir un algorithme simple de calcul de la racine carrée des nombres entiers avec une précision décimale arbitraire. 1.Calcul de la somme des \(n\) premiers entiers naturels impairs Il est,...
Plus de réels que de rationnels : un argument diagonal par les bases de numération
Dans cet article, nous abordons la question du "comptage" des nombres réels, autrement dit de la détermination du cardinal de l'ensemble \(\mathbb R\). Celui-ci est strictement supérieur au cardinal de l'ensemble des nombres rationnels, ce que nous expliquons de deux...
L’irrationalité de √2 : une tragédie pythagoricienne
Les tragédies grecques existaient aussi chez les mathématiciens de l'Antiquité. La découverte de la racine carrée du nombre 2 est le sujet de l'une d'entre elles, qui a trouvé une fin heureuse à l'époque moderne. 1.Un disciple de Pythagore "mesure" la diagonale du...
Connexion
Bienvenue sur La Règle et le Compas ! Pour lire les articles du blog en intégralité, merci de vous connecter. Si ce n'est déjà fait, vous pouvez vous inscrire librement ici sur MATHESIS.
Explorer par Catégories
Algèbre
La théorie mathématique des opérations et des structures
Analyse
La théorie mathématique des processus infinitésimaux
Cinématique
La théorie mathématique du mouvement
Ensembles
La théorie fondamentale des multiplicités mathématiques
Fonctions
La théorie mathématique des relations entre variables
Géométrie
La théorie mathématique des formes et des transformations
Logique
Le traitement mathématique de la logique naturelle
Nombres
La théorie mathématique des nombres et leurs propriétés
Trigonométrie
La théorie mathématique des angles et longueurs
Recherche
Tous les Articles