La Règle et le Compas
Espace Mathématique
Une approche conceptuelle
de la science mathématique
Articles Récents
Théorie mathématique de la musique : II.Gammes, tonalité et harmonie
Si la mélodie et l'harmonie sont les deux dimensions du tissu musical qu'est le contrepoint, l'harmonie désigne la superposition instantanée des...
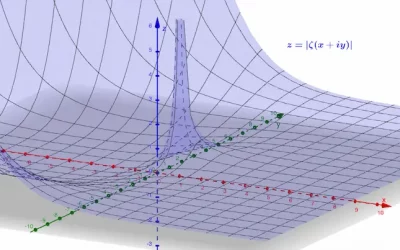
Séries numériques et fonction zeta de Riemann
Les séries de nombres réels et complexes sont une manière alternative de considérer les suites de tels nombres comme sommes infinies de termes....
Théorie mathématique de la musique : I.Mélodie, consonance et chromatisme
On dit, peut-être d'après Platon, que la musique adoucit les mœurs. Vibration mélodique et harmonique, qui trouve son origine culturelle dans la...
L’ontologie première au fondement de la mathématique
Quel est le fondement dernier de la mathématique comme science de l'infini ? Il ne peut s'agir de la logique mathématique, qui renvoie toujours...
Applications et transformations affines du plan euclidien
Les applications affines du plan euclidien sont celles qui préservent sa structure affine, c'est-à-dire essentiellement l'alignement des points et...
Histoire de l’infini II : L’Antiquité et le Moyen Âge théologiques
Nous poursuivons notre revue de l'histoire du concept d'infini dans la tradition occidentale qui précède Cantor, son inventeur mathématique dans la...
Isométries vectorielles du plan euclidien
Histoire de l’infini I : La philosophie grecque antique
Nous proposons une revue de l'histoire du concept d'infini dans la tradition occidentale qui précède Cantor, son inventeur mathématique dans la...
Fonctions continues et théorème des valeurs intermédiaires
Les fonctions continues à valeurs réelles forment le concept fondamental de l'analyse réelle et de la topologie. Or, si la notion de continuité est...
Algèbre Linéaire : la Surprenante Arithmétisation de l’Espace
The Axiom of Infinity: Founding Arithmetic in Set Theory
We explore the foundation of natural arithmetic starting from Peano's axioms within set theory, revealing an innovative approach to conceptualizing...
Fonder l’arithmétique dans la théorie des ensembles
Nous explorons la fondation de l'arithmétique naturelle en partant des axiomes de Peano au sein de la théorie des ensembles, révélant une approche...
Analycité des fonctions holomorphes : indice et formules de Cauchy
Introduction : fonctions holomorphes et analytiques En introduisant les fonctions holomorphes d'une variable complexe, c'est-à-dire dérivables au...
Principes et propriétés des fonctions holomorphes d’une variable complexe
Les principes fondamentaux des fonctions holomorphes d'une variable complexe exploitent la dérivabilité et les caractéristiques uniques qui...
Convergence et limites des fonctions d’une variable réelle
La notion de limite d'une fonction est la base de l'analyse réelle, c'est-à-dire de la théorie des fonctions à valeurs dans l'ensemble $\mathbb R$ :...
Courbes différentiables dans les espaces réels
Dans la géométrie différentielle, l'analyse réelle et la géométrie euclidienne convergent vers une description infinitésimale des objets...
Fonctions monotones d’une variable réelle
Nous revenons dans cet article sur les fonctions monotones d'une variable réelle. Les propriétés de l'analyse des fonctions d'une variable réelle...
The higher axioms of natural set theory
Based on the notions of object and class derived from natural logic, we have redefined the concept of set in an intuitive way, thus establishing a...
Les axiomes supérieurs de la théorie naturelle des ensembles
En nous appuyant sur les notions d'objet et de classe issues de la logique naturelle, nous avons redéfini le concept d'ensemble de manière...
Natural Set Theory: An Ultimate Foundation for Mathematics
The revolution in mathematics is that of set theory, which responds both to the problem of a universal and rigorous conceptual language and to that...
La théorie (naturelle) des ensembles : un fondement ultime pour les mathématiques
La révolution des mathématiques est celle de la théorie des ensembles, qui répond à la fois au problème d'un langage conceptuel universel et...
Structure et topologie de la droite réelle
L'ensemble des nombres réels, quelle que soit la manière dont il est présenté, défini ou construit, n'est pas une multiplicité "amorphe", mais il...
L’intégrale selon Riemann : fonctions continues sur un segment
Quelle est l'opération inverse de la dérivée d'une fonction ? Une première réponse à cette question consiste à intégrer une fonction qu'on veut...
Polynômes irréductibles à coefficients réels et complexes
Les propriétés des polynômes à une indéterminée sur un corps sont analogues à celles des nombres entiers relatifs. En exploitant cette analogie à...
Recherche
Explorer par Catégories
Algèbre
La théorie mathématique des opérations et des structures
Analyse
La théorie mathématique des processus infinitésimaux
Cinématique
La théorie mathématique du mouvement
Ensembles
La théorie fondamentale des multiplicités mathématiques
Fonctions
La théorie mathématique des relations entre variables
Géométrie
La théorie mathématique des formes et des transformations
Logique
Le traitement mathématique de la logique naturelle
Nombres
La théorie mathématique des nombres et leurs propriétés
Trigonométrie
La théorie mathématique des angles et longueurs
Connexion
Bienvenue sur La Règle et le Compas ! Pour lire les articles du blog en intégralité, merci de vous connecter. Si ce n'est déjà fait, vous pouvez vous inscrire librement ici sur MATHESIS.
Tous les Articles