Les séries de nombres réels et complexes sont une manière alternative de considérer les suites de tels nombres comme sommes infinies de termes. Cette représentation des suites est particulièrement appropriée dans la théorie des nombres, où certains nombres sont obtenus comme sommes infinies de nombres rationnels, et dans l’analyse ou théorie des fonctions, où certaines fonctions sont obtenues de même comme sommes infinies de fonctions simples, essentiellement polynomiales. Nous introduisons les séries de nombres réels et complexes avec comme exemple fondamental les séries de Riemann, dont la convergence permet de définir la célèbre fonction zeta de Riemann, qu’on prolonge de manière analytique à une fonction méromorphe du plan complexe. C’est l’occasion de formuler explicitement l’hypothèse de Riemann, conjecture formidable qui constitue le grand problème mathématique de notre temps.

1.Séries de nombres réels et complexes

Rappelons qu’une série de nombres réels ou complexes est une suite, dont les termes sont des sommes finies de nombres. On forme une série à partir d’une suite $(u_n)_{n\geq n_0}$ de nombres réels ou complexes en considérant les sommes $S_n=\sum_{k=n_0}^n u_k$ des termes de la suite $(u_n)$ jusqu’à l’indice $n.$

Définition 1
Si $(u_n)_{n\geq n_0}$ est une suite de nombres réels ou complexes, la série de terme général $u_n$ est la suite $(S_n)_{n\geq n_0}$ des sommes $S_n=\sum_{k=n_0}^n u_k,$ notée $\sum_{k\geq n_0} u_k.$
On dit que la série de terme général $u_n$ converge si la suite $(S_n),$ dont les termes sont appelés sommes partielles de la série, converge.
On dit qu’elle diverge dans le cas contraire. Si la série $\sum_{n\geq n_0} u_n$ converge, la limite $\lim\limits_{n\to\infty} S_n$ est appelée somme de la série, et notée $\sum_{k=n_0}^\infty u_k.$

Si une série $\sum_{n\geq n_0} u_n$ de nombres réels ou complexes converge, alors il en est de même de toute série de la forme $\sum_{n\geq n_1} u_n,$ pour $n_1\geq n_0,$ et réciproquement : supprimer un nombre fini d’éléments au début de la série ne change pas son caractère convergent ou divergent.

Ainsi, pour tout $n_1\geq n_0,$ la série $\sum_{n\geq n_1} u_n$ est convergente, et appelée reste d’ordre $n_1$ de la série convergente $\sum_{n\geq n_0} u_n.$ On démontre également que si une série numérique ou complexe converge, alors son terme général tend vers zéro. Si ce n’est pas le cas, par contraposition elle ne peut converger, et on dit qu’elle est grossièrement divergente.

Exemple 1
L’exemple fondamental de série convergente est celui de la série géométrique de raison un nombre complexe $x$ donné. Il s’agit de la série $\sum_{n\geq 0} x^n,$ dont les sommes partielles valent $S_n=\sum_{k=0}^n x^k=\dfrac{1-x^{k+1}}{1-x}$ si $x\neq 1,$ et $n+1$ si $x=1.$ Si $|x|<1,$ on a $\lim\limits_{n\to\infty} x^{n+1}=0,$ donc la série converge vers $\frac{1}{1-x},$ tandis que si $|x|\geq 1,$ on a $|x^n|=|x|^n,$ donc $x^n$ ne tend pas vers zéro : la série est alors grossièrement divergente.

On dit par ailleurs qu’une série de nombres réels ou complexes $\sum_{n\geq n_0} u_n$ converge absolument si la série de nombre réels positifs $\sum_{n\geq n_0} |u_n|$ converge. On démontre alors qu’une série absolument convergente est convergente, ce qui permet d’établir la convergence de nombreuses séries.

2.La divergence de la série harmonique

Un contre-exemple de série numérique convergente est donné par la série dite harmonique, qui est par définition la série $\sum_{n\geq 1} 1/n.$ Le nom de cette série vient semble-t-il du rapport à la moyenne harmonique, mais on pense aussi à la théorie musicale, où les harmoniques d’un son donné sont les sons dont la fréquence est un multiple entier $n$ de la fréquence du son de base : ces sons sont produits par une corde vibrante dans un rapport de longueur inverse, c’est-à-dire $1/n,$ avec la longueur de la corde produisant le son fondamental. Ainsi, si les harmoniques d’un son sont données par les fréquences de rapport $1,2,3,\ldots,n,$ elles correspondent aux rapports de longueur $1,1/2,1/3,\ldots,1/n,\ldots$ qui sont les termes de la série harmonique.

Pour revenir à nos séries de nombres, la différence des sommes partielles d’indices $2n$ et $n$ de cette série est $S_{2n}-S_n=\sum_{k=n+1}^{2n}1/k$ pour tout entier $n$ non nul, et comme pour tout $k=n+1,\ldots,2n$ on a $1/k\geq 1/2n,$ par récurrence il vient $S_{2n}-S_n\geq 1/2.$ Mais si la série harmonique convergeait, alors les suites $(S_n)$ et $(S_{2n})$ auraient la même limite $S$ — puisque la seconde est une sous-suite de la première — de sorte que la limite de la suite $(S_{2n}-S_n)$ serait nulle, ce qui est précisément impossible si les termes de cette suite sont tous supérieurs à $1/2.$ Ainsi, bien que la série harmonique ne soit pas grossièrement divergente, nous avons démontré :

Proposition 1
La série harmonique $\sum_{n\geq 1} 1/n$ est divergente.

3.Séries de Riemann : convergence et divergence dans le cas réel

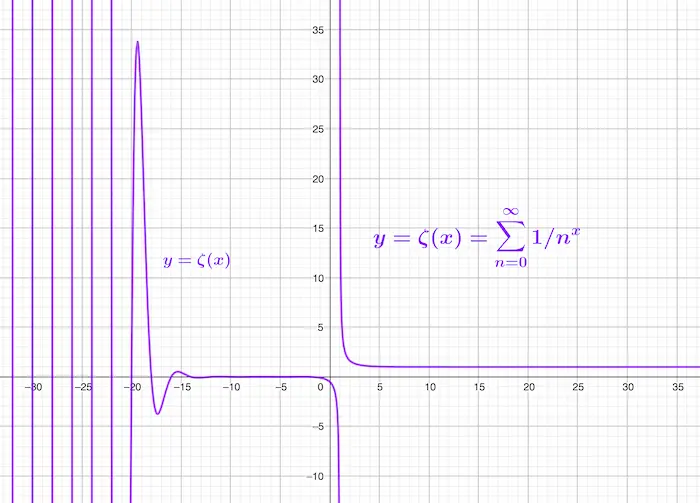
La série harmonique est un cas particulier de série de la forme $\sum_{n\geq 1} 1/n^a,$ où $a$ est un nombre réel strictement positif. En effet, grâce à la fonction exponentielle réelle on peut définir, pour tous $n\in\mathbb N^*$ et $a\in \mathbb R_+^*,$ le nombre réel $n^a:=\exp(a \ln n),$ qui est toujours strictement positif par les propriétés de $\exp.$

Définition 2
La série de Riemann d’indice $a\in\mathbb R_+^*$ est la série numérique $\sum_{n\geq 1} 1/n^a.$

A partir de la comparaison à des séries convergentes ou divergentes, on peut caractériser exactement les nombres réels $a>0$ tels que la série de Riemann d’indice $a$ converge :

Proposition 2
La série de terme général $1/n^a,$ avec $a\in\mathbb R_+^*,$ est convergente si $a>1$ et divergente si $a\leq 1.$

Démontrons-le, en supposant d’abord que $a\leq 1$ : pour tout $n\in\mathbb N^*$ on a $a\ln n\leq \ln n,$ donc $n^a\leq n,$ donc $1/n^a\geq 1/n,$ et par comparaison à la série harmonique, divergente par la proposition 1, la série de terme général $1/n^a$ diverge.

4.La fonction zeta de Riemann

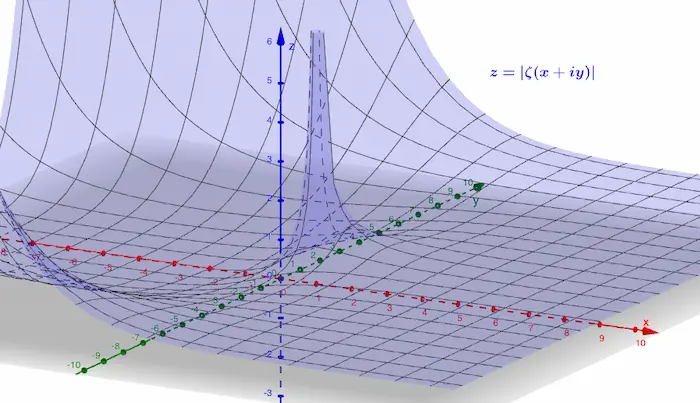
Soient $n\in\mathbb N^*$ et $s=a+ib$ un nombre complexe : grâce à la fonction exponentielle complexe, on peut définir $n^s=\exp(s\ln n),$ de sorte qu’on a $n^s=\exp(a\ln n).\exp(ib\ln n)=n^a.e^{ib\ln n}$ par les propriétés de $\exp:\mathbb C\to \mathbb C^*.$ En particulier, on a $|n^s|=|n^a|=n^a$ puisque $|e^{ib\ln n}|=1$ et $n^a=\exp(a\ln n)>0.$ Par la proposition 2, la série complexe $\sum_{n\geq 1} 1/n^s$ converge donc absolument si $Re(s)=a>1.$ On peut donc, avec Bernhard Riemann, définir par cette série une fonction complexe des nombres de partie réelle $>1$ :

Définition 3
La fonction zeta (de Riemann) est la fonction notée $\zeta:\{z\in \mathbb C : Re(z)>1\}\to\mathbb C,$ qui associe à tout nombre complexe $s$ de partie réelle $Re(s)>1$ le nombre complexe $\zeta(s):=\sum_{n=1}^\infty 1/n^s.$

La série de Riemann $\sum_{n\geq 1} 1/n^s$ d’indice un nombre complexe $s$ est un cas particulier de série de Dirichlet, série de la forme $\sum_{n\geq 1} a_n/n^s,$ où $a_n$ est une série de nombres complexes. Les séries de Dirichlet sont en fait des séries de fonctions ayant la propriété fondamentale suivante :

Proposition 3
Si $S=\sum_{n\geq 1} a_n/n^s$ est une série de Dirichlet, alors il existe un nombre réel $a_0,$ appelée abscisse de convergence de $S,$ tel que la série $S$ converge si $Re(s)>a_0$ et diverge si $Re(s)<a_0,$ et la fonction définie par $F(s):=\sum_{n=1}^\infty a_n/n^s$ sur $\{s\in\mathbb C : Re(s)>a_0\}$ est holomorphe, de dérivées successives $F^{(k)}(s)=\sum_{n\geq 1} a_n(-\ln n)^k/n^s$ pour tout entier $k\geq 1.$

On peut alors démontrer que la série de Riemann $\sum_{n\geq 1} 1/n^s$ a pour abscisse de convergence $1,$ et la fonction zeta $\zeta:\{s\in\mathbb C : Re(s)>1\}\to\mathbb C$ est donc holomorphe, de dérivées successives $\zeta^{(k)}(s)=\sum_{n\geq 1} (-\ln n)^k/n^s.$

5.Prolongement analytique de la fonction zeta

Rappelons qu’une partie ouverte $U$ du plan complexe $\mathbb C$ est dite connexe, si deux points quelconques $z,w\in U$ sont reliés par un chemin dans $U$ : il existe une fonction continue $f:[0,1]\to U,$ appelée chemin ou arc, telle que $f(0)=z$ et $f(1)=w.$ Cette propriété est du moins la connexité par arcs, équivalente à la connexité dans le plan complexe. On étudie en général les fonctions holomorphes sur des ouverts connexes, appelés aussi domaines, où l’on peut décrire leurs propriétés analytiques.

Définition 4
Soit $f:U\to\mathbb C$ une fonction holomorphe définie sur un ouvert du plan complexe. Si $V$ est un ouvert contenant $U,$ une fonction holomorphe $g:V\to \mathbb C$ dont la restriction $g|_U$ à $U$ est le fonction $f,$ est appelée prolongement analytique de $U.$

On démontre alors, dans le Principe des zéros isolés, que si un prolongement analytique existe sur un ouvert connexe, ce prolongement est nécessairement unique. En utilisant la fonction êta de Dirichlet, construite à partir de la série de Dirichlet $\sum_{n\geq 1} (-1)^{n-1}/n^s$ d’abscisse de convergence $0,$ on prolonge la fonction $\zeta$ au demi-plan des nombres complexes de partie réelle $>0$ et différents de $1.$

En utilisant alors la fonction Gamma d’Euler, extension de la factorielle des entiers aux complexe $s$ tels que $Re(s)>0$ par la formule $\Gamma(s)=\int_0^\infty e^{-t} t^{s-1}\ dt,$ et prolongée en une fonction holomorphe sur $\mathbb C\setminus\mathbb Z^-=\{s\in\mathbb C : s\neq 0,-1,-2,-3,\ldots\},$ Riemann démontre le théorème suivant :

Théorème 1
La fonction $\zeta:\{s\in \mathbb C : Re(s)>0\}\to\mathbb C$ admet un prolongement analytique sur le domaine $\mathbb C\setminus\{1\}.$

En définissant avec Riemann la fonction entière $\xi(s):=(1/2)s(s-1)\pi^{-s/2}\Gamma(s/2)\zeta(s)$ — toutes les singularités liées aux fonctions méromorphes $\Gamma$ et $\zeta$ sont compensées — on obtient alors une égalité fonctionnelle valable pour tout $s\in\mathbb C,$ à savoir $\xi(s)=\xi(1-s).$

6.L’hypothèse de Riemann

Le prolongement de la fonction zeta de Riemann n’est plus décrit, en général, par la série de Riemann $\sum_{n\geq 1} 1/n^s$ sur tout le domaine $\mathbb C-\{1\},$ puisque la série diverge pour $Re(s)<1.$ Elle constitue toutefois un objet mathématique aux propriétés arithmétiques remarquables, liées à la distribution des nombres premiers.

Cela se voit par exemple dans l’expression qu’en donne Euler pour $Re(s)>1$ : le nombre $\zeta(s)$ est alors également donné par un produit infini, sous la forme $\zeta(s)=\prod_p (1-1/p^s)^{-1},$ où le produit est pris sur tous les nombres premiers $p.$ On en déduit alors la propriété suivante :

Proposition 4
La fonction zeta de Riemann n’a pas de zéros sur l’ensemble $\{s\in\mathbb C : Re(s)>1\}.$

Le théorème suivant, démontré à la fois par Hadamard et La Vallée-Poussin, permet d’exclure également les nombres complexes de partie réelle $1$ :

Théorème 2
La fonction $\zeta$ de Riemann n’a pas de zéros sur la droite verticale d’équation $x=1.$

Par ailleurs, grâce à l’équation fonctionnelle entre produits de fonctions méromorphes $\zeta(s)=2^s\pi^{s-1}\sin(\pi/2)\Gamma(1-s)\zeta(1-s),$ on montre également que les zéros de la fonction $\zeta$ se répartissent en deux catégories :

1. Les zéros dits « triviaux », c’est-à-dire les nombres entiers de la forme $-2n$ pour $n\in \mathbb N^*$
2. Les autres zéros, non triviaux, qui sont les zéros de la fonction $\xi$ de Riemann, et qui sont donc symétriques par rapport à la droite verticale d’équation $x=1/2.$

Par la proposition 4 et le théorème 2, les zéros non triviaux de la fonction $\zeta$ se trouvent donc dans la bande $\{s\in\mathbb C : 0<Re(s)<1.\}$

Or, les innombrables solutions de l’équation $\zeta(s)=0$ identifiées depuis Riemann jusqu’à ce jour sont toutes situées sur la droite verticale d’équation $x=1/2.$ Ainsi le grand mathématicien formulait-il sa célèbre hypothèse, conjecture formidable qui n’est encore ni démontrée, ni réfutée :

Conjecture (Hypothèse de Riemann)
Tous les zéros non triviaux de la fonction $\zeta : \mathbb C-\{1\}\to \mathbb C$ sont situés sur la droite verticale d’équation $x=1/2.$